《2025年阳光课堂金牌练习册七年级数学上册人教版》

7. 如图,$A,B$为数轴上的两点,点$A表示的数为-2$,点$B表示的数为-6$.现有一只电子蚂蚁从点$B$出发,沿数轴以每秒2个单位长度的速度向右运动.
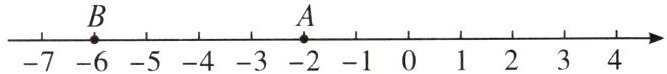
(1)经过$t\mathrm{s}$后,用含$t$的代数式表示电子蚂蚁所在的位置表示的数.
(2)当$t$为何值时,电子蚂蚁所在的位置到点$A$的距离为2个单位长度？

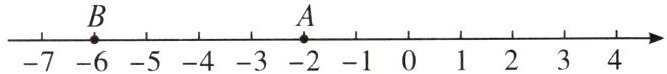
答案：
(1)根据题意，得经过t s后，电子蚂蚁所在的位置表示的数为2t-6.
(2)|-2-(-6)|÷2=2(s).当电子蚂蚁在点 A 的左侧，即t＜2时，-2-(2t-6)=2，解得t=1；当电子蚂蚁在点 A 的右侧，即t＞2时，2t-6-(-2)=2，解得t=3.故当t=1或t=3时，电子蚂蚁所在的位置到点 A 的距离为2个单位长度.

8. 定义一种新运算“$\oplus$”：$m\oplus n= 3n-2m+1$,比如,$4\oplus(-5)= 3×(-5)-2×4+1= -22$.
(1)求$(-3)\oplus2$的值；
(2)已知$(3x-1)\oplus(x+3)= 6$,求$x$的值.

答案：
(1)因为m⊕n=3n-2m+1，所以(-3)⊕2=3×2-2×(-3)+1=6-(-6)+1=13.
(2)因为m⊕n=3n-2m+1,(3x-1)⊕(x+3)=6，所以3(x+3)-2(3x-1)+1=6，解得x=2.

【典型例题】解下列方程：
(1) $ 3 - \dfrac{x - 1}{2} = 3x - 1 $；
(2) $ x - \dfrac{x - 1}{2} = 2 - \dfrac{x + 2}{3} $.

答案：
(1)
去分母：方程两边同乘$2$，得$6 - (x - 1) = 2(3x - 1)$；
去括号：得$6 - x + 1 = 6x - 2$；
移项：得$-x - 6x = -2 - 6 - 1$；
合并同类项：得$-7x = -9$；
系数化为$1$：得$x = \dfrac{9}{7}$。
(2)
去分母：方程两边同乘$6$，得$6x - 3(x - 1) = 12 - 2(x + 2)$；
去括号：得$6x - 3x + 3 = 12 - 2x - 4$；
移项：得$6x - 3x + 2x = 12 - 4 - 3$；
合并同类项：得$5x = 5$；
系数化为$1$：得$x = 1$。