《2025年阳光课堂金牌练习册七年级数学上册人教版》

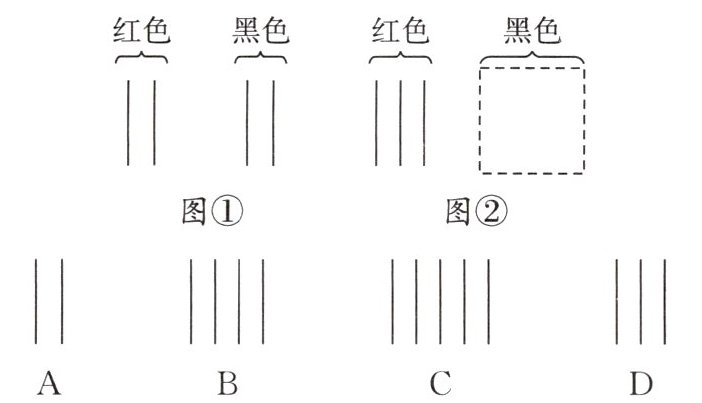
4. 中国人很早就开始使用负数,魏晋时期的数学家刘徽在为《九章算术》作注时,用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(红色为正,黑色为负)。现用算筹表示加法运算,如图①,它表示的是 $(+2) + (-2)$。根据这种表示法,如图②,它所表示的算式是 $(+3) + (-4)$,由此可推算出图②被盖住的部分是(B)

答案： B【解析】因为题中图①表示的是$(+2)+(-2)$，所以$(+3)+(-4)$表示的应该是3根红色的算筹加上4根黑色的算筹.

5. 绝对值不大于 $4$ 的所有整数的和是(B)
A.$16$
B.$0$
C.$576$
D.$-1$

答案： B【解析】绝对值不大于4的所有整数有：0，±1，±2，±3，±4，它们的和为0.

6. 有一批食品罐头,每听标准质量为 $454$ g,现抽取 $10$ 听样品进行检测,结果如下表(单位：g)：

这 $10$ 听罐头的总质量是多少？

答案： 6.【解】方法一：$444+459+454+459+454+454+449+454+459+464=4550(g)$.
方法二：把每听罐头超过454g的克数用正数表示，不足的克数用负数表示，10听罐头对应的数分别为-10，+5，0，+5，0，0，-5，0，+5，+10.
$(-10)+5+0+5+0+0+(-5)+0+5+10=[(-10)+10]+[(-5)+5]+(5+5)=10(g)$.
$454×10+10=4540+10=4550(g)$.
答：这10听罐头的总质量为4550g.

7. $(-5\frac{5}{6}) + (-9\frac{2}{3}) + 17\frac{3}{4} + (-3\frac{1}{2})$ 可以按如下方法计算：原式 $= [(-5) + (-\frac{5}{6})] + [(-9) + (-\frac{2}{3})] + (17 + \frac{3}{4}) + [(-3) + (-\frac{1}{2})] = [(-5) + (-9) + 17 + (-3)] + [(-\frac{5}{6}) + (-\frac{2}{3}) + \frac{3}{4} + (-\frac{1}{2})] = 0 + (-1\frac{1}{4}) = -1\frac{1}{4}$。
上面这种方法叫拆项法,仿照上面的方法,计算下面的式子。
$(-2024\frac{5}{6}) + (-2025\frac{1}{2}) + 4050\frac{3}{4} + (-1\frac{1}{2})$。

答案： 7.【解】$(-2024\frac{5}{6})+(-2025\frac{1}{2})+4050\frac{3}{4}+(-1\frac{1}{2})$
$=[(-2024)+(-\frac{5}{6})]+[(-2025)+(-\frac{1}{2})]+(4050+\frac{3}{4})+[(-1)+(-\frac{1}{2})]$
$=[(-2024)+(-2025)+4050+(-1)]+[(-\frac{5}{6})+(-\frac{1}{2})+\frac{3}{4}+(-\frac{1}{2})]$
$=0+(-1\frac{1}{12})=-1\frac{1}{12}$.