第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
在$|-2|$,$-|-2|$,$-(-2)$,$-|2|$中,等于 2 的数有(
A.1 个
B.2 个
C.3 个
D.4 个
B
)A.1 个
B.2 个
C.3 个
D.4 个
答案:
B【解析】先化简各数,再和2进行比较.因为|-2|=2,-|-2|=-2,-(-2)=2,-|2|=-2,所以等于2的数有2个.
1. $-\frac{2}{7}$的绝对值是(
A.$\frac{2}{7}$
B.$\frac{7}{2}$
C.$-\frac{2}{7}$
D.$-\frac{7}{2}$
A
)A.$\frac{2}{7}$
B.$\frac{7}{2}$
C.$-\frac{2}{7}$
D.$-\frac{7}{2}$
答案:
A
2. 下列各式中成立的是(
A.$-(+3)= 3$
B.$-(-2)= +(-2)$
C.$-|-4|= 4$
D.$-|+5|= -|-5|$
D
)A.$-(+3)= 3$
B.$-(-2)= +(-2)$
C.$-|-4|= 4$
D.$-|+5|= -|-5|$
答案:
D【解析】A.-(+3)=-3≠3,不符合题意;B.因为-(-2)=2,+(-2)=-2,所以-(-2)≠+(-2),不符合题意;C.-|-4|=-4≠4,不符合题意;D.因为-|+5|=-5,-|-5|=-5,所以-|+5|=-|-5|,符合题意.
3. 下列说法错误的是(
A.表示$-3的点与原点的距离是|-3|$
B.一个有理数的绝对值一定是正数
C.一个有理数的绝对值一定不是负数
D.互为相反数的两个数绝对值一定相等
B
)A.表示$-3的点与原点的距离是|-3|$
B.一个有理数的绝对值一定是正数
C.一个有理数的绝对值一定不是负数
D.互为相反数的两个数绝对值一定相等
答案:
B【解析】A.根据绝对值的意义,|-3|表示“在数轴上,表示-3的点与原点的距离”,故本选项正确,不符合题意;B.若这个有理数为0,则0的绝对值还是0,本选项错误,符合题意;C.根据绝对值的意义,有理数a的绝对值|a|表示“在数轴上,表示a的点与原点的距离”,故任意有理数的绝对值为非负数,不可能为负数,本选项正确,不符合题意;D.根据相反数的定义,可知表示互为相反数的两个数的点与原点的距离相等,本选项正确,不符合题意.
4. 一批零件超过规定长度记为正数,不足规定长度记为负数,越接近规定长度质量越好. 检查这批零件中的四个,结果如下:第一个为$0.05\mathrm{mm}$,第二个为$-0.02\mathrm{mm}$,第三个为$-0.04\mathrm{mm}$,第四个为$0.03\mathrm{mm}$,则这四个零件中质量最好的是(
A.第一个
B.第二个
C.第三个
D.第四个
B
)A.第一个
B.第二个
C.第三个
D.第四个
答案:
B【解析】因为|-0.02|<|0.03|<|-0.04|<|0.05|,所以质量最好的零件是第二个.
5. 如图,数轴上的数$a的绝对值是数b$的绝对值的 3 倍,则此数轴的原点是(
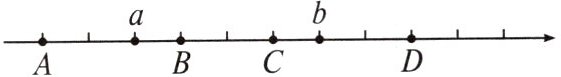
A.点$A$
B.点$A或点B$
C.点$C$
D.点$C或点D$
D
)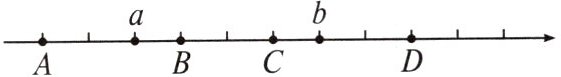
A.点$A$
B.点$A或点B$
C.点$C$
D.点$C或点D$
答案:
D【解析】由题图知,表示数a,b的点之间的距离是4个单位长度.①当a>0,b>0时,由题意可得|a|=3|b|,不符合实际情况;②当a<0,b<0时,由题意可得|a|=3|b|,可得a=-6,b=-2,故数轴的原点在点D处;③当a<0,b>0时,由题意可得|a|=3|b|,可得a=-3,b=1,故数轴的原点在点C处.综上可得,数轴的原点在点C或点D处.
6. 如果两个有理数的绝对值分别是 3 和 1,那么在数轴上,表示这两个有理数的点相距多少个单位长度?
答案:
【解】若设有理数a的绝对值等于3,则a=3或a=-3;若设有理数b的绝对值等于1,则b=1或b=-1.当a=3,b=1时,表示有理数a,b的点相距2个单位长度;当a=3,b=-1时,表示有理数a,b的点相距4个单位长度;当a=-3,b=1时,表示有理数a,b的点相距4个单位长度;当a=-3,b=-1时,表示有理数a,b的点相距2个单位长度.综上所述,表示这两个有理数的点相距2个单位长度或4个单位长度.
7. 绝对值大于 2.5 且小于 5.1 的负整数有哪些?请分别写出.
答案:
【解】设x的绝对值大于2.5且小于5.1,且x为整数,则有2.5<|x|<5.1.所以|x|=3,4,5,所以绝对值大于2.5且小于5.1的所有负整数为-3,-4,-5.
【典型例题1】比较下列各组数的大小:
(1)$-\dfrac{5}{6}和-\dfrac{6}{7}$;(2)$-\dfrac{22}{7}和-3.13$;
(3)$-|-5|与0$;(4)$-(-\dfrac{1}{5})与-|-\dfrac{1}{6}|$.
(1)$-\dfrac{5}{6}和-\dfrac{6}{7}$;(2)$-\dfrac{22}{7}和-3.13$;
(3)$-|-5|与0$;(4)$-(-\dfrac{1}{5})与-|-\dfrac{1}{6}|$.
答案:
答题卡:
(1)
$|-\dfrac{5}{6}| = \dfrac{5}{6} = \dfrac{35}{42}$,
$|-\dfrac{6}{7}| = \dfrac{6}{7} = \dfrac{36}{42}$,
因为 $\dfrac{35}{42} \lt \dfrac{36}{42}$,
所以 $-\dfrac{5}{6} \gt -\dfrac{6}{7}$。
(2)
$|-\dfrac{22}{7}| = \dfrac{22}{7} \approx 3.1429$,
$|-3.13| = 3.13$,
因为 $3.1429 \gt 3.13$,
所以 $-\dfrac{22}{7} \lt -3.13$。
(3)
$-|-5| = -5$,
因为 $-5 \lt 0$,
所以 $-|-5| \lt 0$。
(4)
$-(-\dfrac{1}{5}) = \dfrac{1}{5}$,
$-|-\dfrac{1}{6}| = -\dfrac{1}{6}$,
因为 $\dfrac{1}{5} \gt -\dfrac{1}{6}$,
所以 $-(-\dfrac{1}{5}) \gt -|-\dfrac{1}{6}|$。
(1)
$|-\dfrac{5}{6}| = \dfrac{5}{6} = \dfrac{35}{42}$,
$|-\dfrac{6}{7}| = \dfrac{6}{7} = \dfrac{36}{42}$,
因为 $\dfrac{35}{42} \lt \dfrac{36}{42}$,
所以 $-\dfrac{5}{6} \gt -\dfrac{6}{7}$。
(2)
$|-\dfrac{22}{7}| = \dfrac{22}{7} \approx 3.1429$,
$|-3.13| = 3.13$,
因为 $3.1429 \gt 3.13$,
所以 $-\dfrac{22}{7} \lt -3.13$。
(3)
$-|-5| = -5$,
因为 $-5 \lt 0$,
所以 $-|-5| \lt 0$。
(4)
$-(-\dfrac{1}{5}) = \dfrac{1}{5}$,
$-|-\dfrac{1}{6}| = -\dfrac{1}{6}$,
因为 $\dfrac{1}{5} \gt -\dfrac{1}{6}$,
所以 $-(-\dfrac{1}{5}) \gt -|-\dfrac{1}{6}|$。
查看更多完整答案,请扫码查看


