《2025年时习之暑假衔接七年级数学人教版》

3.如图是甲、乙、丙三人玩跷跷板的示意图(支点在跷跷板中点处),已知乙、丙的体重,则甲的体重的取值范围在数轴上表示正确的是( )

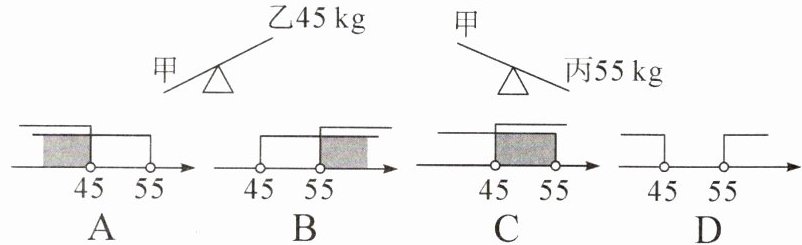
答案： C

4.若关于x的一元一次不等式组$\left\{\begin{array}{l} x-3＜0,\\ x-a＞1\end{array} \right. $无解,则a的取值范围是( )

A.$a\geqslant 2$
B.$a＞2$
C.$a\leqslant -2$
D.$a＜-2$

答案： A

5.不等式组$2\leqslant 3x-7＜8$的解集是____。

答案： $3\leqslant x＜5$

6.在平面直角坐标系中,若点$P(a-3,a+1)$在第二象限,则a的取值范围为____。

答案： $-1\lt a＜3$

7.不等式组$\left\{\begin{array}{l} x+2＞a,\\ x-1＜b\end{array} \right. 的解集是1＜x＜2$,则$a= $____,$b= $____。

答案： 3 1

8.解下列不等式组,并把其解集在数轴上表示出来。
(1)$\left\{\begin{array}{l} 2x-1＞x+1,\\ x+8＞4x-1;\end{array} \right. $
(2)$\left\{\begin{array}{l} 2x-3＜1,\\ \frac {x-1}{2}+2＞-1.\end{array} \right. $

答案：
(1)$2\lt x＜3$，在数轴上表示略.
(2)$-5\lt x＜2$，在数轴上表示略.

9.解不等式组$\left\{\begin{array}{l} 3x+2\leqslant 2(x+3),\\ \frac {3x-1}{2}＞\frac {x}{2},\end{array} \right. $并写出该不等式组的所有整数解。

答案： 解不等式组得$\dfrac{1}{2}\lt x\leqslant4$，故其整数解为1，2，3，4.

10.在武汉市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板。经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元。
(1)求购买一台电脑和一台电子白板各需多少万元；
(2)根据学校实际需求,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低。

答案：
(1)设买一台电脑和一台电子白板各需x万元、y万元.由题意可知$\begin{cases}x+2y=3.5,\\2x+y=2.5,\end{cases}$解得$\begin{cases}x=0.5,\\y=1.5.\end{cases}$故购买一台电脑和一台电子白板各需0.5万元、1.5万元.
(2)设购进电脑a台，则购进电子白板$(30-a)$台.由题意可知$\begin{cases}0.5a+1.5(30-a)\leqslant30,\\0.5a+1.5(30-a)\geqslant28.\end{cases}$解得$15\leqslant a\leqslant17$，因为a为正整数，所以$a=15$或16或17，共有3种方案.$a=15$时，$0.5a+1.5(30-a)=45-a=30$(万元)；$a=16$时，$0.5a+1.5(30-a)=29$(万元)；$a=17$时，$0.5a+1.5(30-a)=28$(万元).故购进17台电脑，13台电子白板时费用最低.

1.不等式组$\left\{\begin{array}{l} x+1＞0,\\ 1-\frac {1}{3}x＞0\end{array} \right. $的解集在数轴上表示正确的是( )

答案： A

2.如果点$P(a-3,a+1)$在第三象限,那么a的取值范围是( )

A.$a＞-1$
B.$a＜3$
C.$-3＜a＜3$
D.$a＜-1$

答案： D

3.若不等式组$2＜x＜a$的整数解恰有3个,则a的取值范围是( )

A.$a＞5$
B.$5＜a＜6$
C.$5\leqslant a＜6$
D.$5＜a\leqslant 6$

答案： D