《2025年时习之暑假衔接七年级数学人教版》

3.如图,已知直线$AB$,$CD相交于点O$,$OE平分\angle COB$.若$\angle BOD= 70^{\circ}$,则$\angle COE$的度数是( )

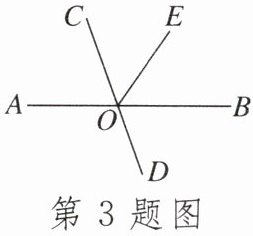
A.$45^{\circ}$
B.$70^{\circ}$
C.$55^{\circ}$
D.$110^{\circ}$

答案： C

4.如图,有两堵围墙,有人想测量地面上两堵围墙内所形成的$\angle AOB$的度数,但人又不能进入围墙,只能站在墙外,请问聪明的你,想求$\angle AOB$,可以先求它的______.

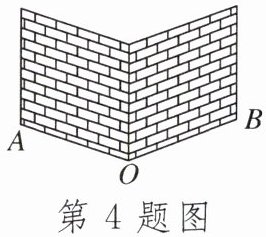
答案： 邻补角或对顶角

5.如图,直线$AB与CD相交于点O$.若$\angle AOD+\angle BOC= 280^{\circ}$,则$\angle AOC$的度数为______.

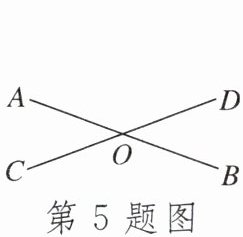
答案： $40^{\circ }$

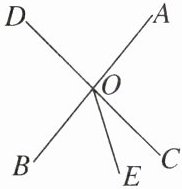
6.如图,直线$AB$,$CD相交于点O$,$OE把\angle BOC$分成两部分.
(1)图中$\angle AOC$的对顶角为______,$\angle AOC$的邻补角为______;
(2)若$\angle AOD= 84^{\circ}$,且$\angle BOE:\angle COE= 3:1$,求$\angle AOE$的度数.

答案：
(1)$∠BOD$ $∠AOD$和$∠BOC$
(2)$\because ∠BOC=∠AOD=84^{\circ },∠BOE:∠COE=3:1,$
$\therefore ∠BOE=\frac {3}{4}∠BOC=63^{\circ }.\therefore ∠AOE=180^{\circ }-∠BOE=180^{\circ }-$
$63^{\circ }=117^{\circ }.$

7.过点$P向线段AB$所在直线画垂线,画图正确的是( )

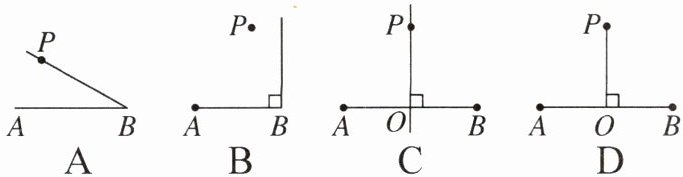
答案： C

8.如图是某跳远运动员在一次比赛中跳远时沙坑的示意图,测量成绩时先使皮尺从后脚脚跟的点$A处开始并与起跳线l垂直于点B$,然后记录$AB$的长度,这样做的理由是( )


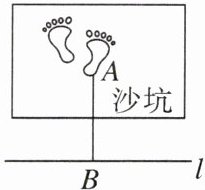
A.过一点可以作无数条直线
B.垂线段最短
C.过两点有且只有一条直线
D.两点之间线段最短

答案： B

9.如图,直线$AB$,$CD相交于点O$,$OE\perp AB$,$\angle EOD= 35^{\circ}$,则$\angle COA$的度数是( )


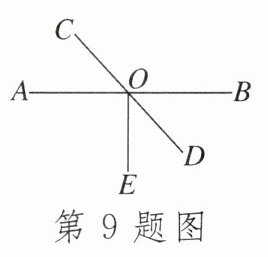
A.$75^{\circ}$
B.$65^{\circ}$
C.$55^{\circ}$
D.$45^{\circ}$

答案： C

10.如图,在三角形$ABC$中,$\angle ACB= 90^{\circ}$,$AC= 8cm$,$BC= 6cm$,$AB= 10cm$.点$D为线段AB$上一动点,则点$C到点D$的最短距离为______$cm$,并在图中作出此时的线段$CD$.

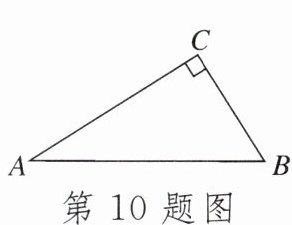
答案： 4.8 作$CD⊥AB$,垂足为 D,图略.

11.如图,已知直线$AB$,$CD$,$EF相交于点O$,$AB\perp CD$,$OG平分\angle AOE$,$\angle FOD= 28^{\circ}$,求$\angle AOG$的度数.

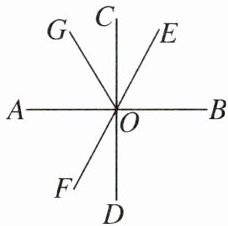
答案： $\because AB⊥CD,\therefore ∠AOC=90^{\circ }$.又$\because ∠COE=∠FOD=28^{\circ },$
$\therefore ∠AOE=∠AOC+∠COE=118^{\circ }.\because OG$平分$∠AOE,$
$\therefore ∠AOG=\frac {1}{2}∠AOE=\frac {1}{2}×118^{\circ }=59^{\circ }.$

12.如图,按角的位置关系填空:$\angle1与\angle2$是______角,$\angle1与\angle3$是______角,$\angle2与\angle3$是______角.

答案： 同旁内 内错 邻补