2025年暑假总动员宁夏人民教育出版社七年级数学沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假总动员宁夏人民教育出版社七年级数学沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
21. 如图,已知数轴上点 $ A $ 表示的数为 8,$ B $ 是数轴上位于点 $ A $ 左侧的一点,且 $ AB = 14 $。动点 $ P $ 从点 $ A $ 出发,以每秒 5 个单位长度的速度沿数轴向左匀速运动,设运动时间为 $ t $ 秒。

(1)数轴上点 $ B $ 表示的数为
(2)动点 $ Q $ 从点 $ B $ 出发,以每秒 3 个单位长度的速度沿数轴向左匀速运动,且点 $ P $,$ Q $ 同时出发。问点 $ P $ 运动多少秒时,$ BQ = BP $?
(3)若 $ M $ 为 $ AP $ 的中点,$ N $ 为 $ BP $ 的中点,则在点 $ P $ 运动的过程中,线段 $ MN $ 的长度是否会发生变化?若会变化,请说明理由;若不会变化,请求出线段 $ MN $ 的长。

(1)数轴上点 $ B $ 表示的数为
-6
,点 $ P $ 表示的数为8 - 5t
(用含 $ t $ 的式子表示)。(2)动点 $ Q $ 从点 $ B $ 出发,以每秒 3 个单位长度的速度沿数轴向左匀速运动,且点 $ P $,$ Q $ 同时出发。问点 $ P $ 运动多少秒时,$ BQ = BP $?
(3)若 $ M $ 为 $ AP $ 的中点,$ N $ 为 $ BP $ 的中点,则在点 $ P $ 运动的过程中,线段 $ MN $ 的长度是否会发生变化?若会变化,请说明理由;若不会变化,请求出线段 $ MN $ 的长。
答案:
(1)-6 $8 - 5t$ 解析:因为点 A 表示的数为 8,B 是数轴上位于点 A 左侧的一点,$AB = 14$,所以点 B 表示的数为$8 - 14 = - 6$.因为动点 P 从点 A 出发,以每秒 5 个单位长度的速度沿数轴向左匀速运动,所以点 P 表示的数为$8 - 5t$.故答案为$- 6;8 - 5t$.
(2)由题意得$|8 - 5t - (- 6)| = 3t$,解得$t = \frac{7}{4}$或$t = 7$.
(3)线段 MN 的长度不会发生改变:①当点 P 在点 A、B 两点之间运动时,$MN = MP + NP = \frac{1}{2}AB = \frac{1}{2}×14 = 7$;②当点 P 运动到点 B 的左侧时,$MN = MP - NP = \frac{1}{2}AP - \frac{1}{2}BP = \frac{1}{2}(AP - BP) = \frac{1}{2}AB = \frac{1}{2}×14 = 7$,所以线段 MN 的长度不变,为 7.
(1)-6 $8 - 5t$ 解析:因为点 A 表示的数为 8,B 是数轴上位于点 A 左侧的一点,$AB = 14$,所以点 B 表示的数为$8 - 14 = - 6$.因为动点 P 从点 A 出发,以每秒 5 个单位长度的速度沿数轴向左匀速运动,所以点 P 表示的数为$8 - 5t$.故答案为$- 6;8 - 5t$.
(2)由题意得$|8 - 5t - (- 6)| = 3t$,解得$t = \frac{7}{4}$或$t = 7$.
(3)线段 MN 的长度不会发生改变:①当点 P 在点 A、B 两点之间运动时,$MN = MP + NP = \frac{1}{2}AB = \frac{1}{2}×14 = 7$;②当点 P 运动到点 B 的左侧时,$MN = MP - NP = \frac{1}{2}AP - \frac{1}{2}BP = \frac{1}{2}(AP - BP) = \frac{1}{2}AB = \frac{1}{2}×14 = 7$,所以线段 MN 的长度不变,为 7.
22. 如图,直线 $ AC // BD $,连接 $ AB $,直线 $ AC $,$ BD $ 及线段 $ AB $ 把平面分成①,②,③,④四个部分,规定:线上各点不属于任何部分。当动点 $ P $ 落在某个部分时,连接 $ PA $,$ PB $,构成 $ \angle PAC $,$ \angle APB $,$ \angle PBD $ 三个角。(提示:有公共端点的两条重合的射线所组成的角是 $ 0^\circ $ 角)
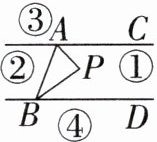
(1)当动点 $ P $ 落在第①部分时,求证:$ \angle APB = \angle PAC + \angle PBD $。
证明:延长 BP 交直线 AC 于点 E,如图①.因为$AC// BD$,所以$∠PEA = ∠PBD$.因为$∠APB = 180^{\circ } - ∠APE = 180^{\circ } - (180^{\circ } - ∠PAE - ∠AEP) = ∠PAE + ∠AEP$,所以$∠APB = ∠PAC + ∠PBD$.

(2)当动点 $ P $ 落在第②部分时,$ \angle APB = \angle PAC + \angle PBD $ 是否成立?(直接回答成立或不成立)
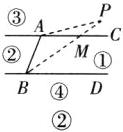
(3)当动点 $ P $ 落在第③部分时,全面探究 $ \angle PAC $,$ \angle APB $,$ \angle PBD $ 之间的关系,并写出动点 $ P $ 的具体位置和相应的结论。选择其中一种结论加以证明。
①当动点 P 在射线 BA 的右侧时,结论:$∠PBD = ∠PAC + ∠APB$.
②当动点 P 在射线 BA 上时,结论:$∠PBD = ∠PAC + ∠APB$或$∠PAC = ∠PBD + ∠APB$或$∠APB = 0^{\circ },∠PAC = ∠PBD$(任写一个即可).
③当动点 P 在射线 BA 的左侧时,结论:$∠PAC = ∠APB + ∠PBD$.
选择①证明:
如图②,连接 PA,连接 PB 交 AC 于点 M.因为$AC// BD$,所以$∠PMC = ∠PBD$.又因为$∠PMC = 180^{\circ } - ∠AMP = ∠PAM + ∠APM$,所以$∠PBD = ∠PAC + ∠APB$.

(1)当动点 $ P $ 落在第①部分时,求证:$ \angle APB = \angle PAC + \angle PBD $。
证明:延长 BP 交直线 AC 于点 E,如图①.因为$AC// BD$,所以$∠PEA = ∠PBD$.因为$∠APB = 180^{\circ } - ∠APE = 180^{\circ } - (180^{\circ } - ∠PAE - ∠AEP) = ∠PAE + ∠AEP$,所以$∠APB = ∠PAC + ∠PBD$.

(2)当动点 $ P $ 落在第②部分时,$ \angle APB = \angle PAC + \angle PBD $ 是否成立?(直接回答成立或不成立)
不成立
(3)当动点 $ P $ 落在第③部分时,全面探究 $ \angle PAC $,$ \angle APB $,$ \angle PBD $ 之间的关系,并写出动点 $ P $ 的具体位置和相应的结论。选择其中一种结论加以证明。
①当动点 P 在射线 BA 的右侧时,结论:$∠PBD = ∠PAC + ∠APB$.
②当动点 P 在射线 BA 上时,结论:$∠PBD = ∠PAC + ∠APB$或$∠PAC = ∠PBD + ∠APB$或$∠APB = 0^{\circ },∠PAC = ∠PBD$(任写一个即可).
③当动点 P 在射线 BA 的左侧时,结论:$∠PAC = ∠APB + ∠PBD$.
选择①证明:
如图②,连接 PA,连接 PB 交 AC 于点 M.因为$AC// BD$,所以$∠PMC = ∠PBD$.又因为$∠PMC = 180^{\circ } - ∠AMP = ∠PAM + ∠APM$,所以$∠PBD = ∠PAC + ∠APB$.

答案:
(1)延长 BP 交直线 AC 于点 E,如图①.因为$AC// BD$,所以$∠PEA = ∠PBD$.因为$∠APB = 180^{\circ } - ∠APE = 180^{\circ } - (180^{\circ } - ∠PAE - ∠AEP) = ∠PAE + ∠AEP$,所以$∠APB = ∠PAC + ∠PBD$.

(2)不成立.
(3)①当动点 P 在射线 BA 的右侧时,结论:$∠PBD = ∠PAC + ∠APB$.
②当动点 P 在射线 BA 上时,结论:$∠PBD = ∠PAC + ∠APB$或$∠PAC = ∠PBD + ∠APB$或$∠APB = 0^{\circ },∠PAC = ∠PBD$(任写一个即可).
③当动点 P 在射线 BA 的左侧时,结论:$∠PAC = ∠APB + ∠PBD$.
选择①证明:
如图②,连接 PA,连接 PB 交 AC 于点 M.因为$AC// BD$,所以$∠PMC = ∠PBD$.又因为$∠PMC = 180^{\circ } - ∠AMP = ∠PAM + ∠APM$,所以$∠PBD = ∠PAC + ∠APB$.

(1)延长 BP 交直线 AC 于点 E,如图①.因为$AC// BD$,所以$∠PEA = ∠PBD$.因为$∠APB = 180^{\circ } - ∠APE = 180^{\circ } - (180^{\circ } - ∠PAE - ∠AEP) = ∠PAE + ∠AEP$,所以$∠APB = ∠PAC + ∠PBD$.

(2)不成立.
(3)①当动点 P 在射线 BA 的右侧时,结论:$∠PBD = ∠PAC + ∠APB$.
②当动点 P 在射线 BA 上时,结论:$∠PBD = ∠PAC + ∠APB$或$∠PAC = ∠PBD + ∠APB$或$∠APB = 0^{\circ },∠PAC = ∠PBD$(任写一个即可).
③当动点 P 在射线 BA 的左侧时,结论:$∠PAC = ∠APB + ∠PBD$.
选择①证明:
如图②,连接 PA,连接 PB 交 AC 于点 M.因为$AC// BD$,所以$∠PMC = ∠PBD$.又因为$∠PMC = 180^{\circ } - ∠AMP = ∠PAM + ∠APM$,所以$∠PBD = ∠PAC + ∠APB$.

查看更多完整答案,请扫码查看


