2025年暑假总动员宁夏人民教育出版社七年级数学沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假总动员宁夏人民教育出版社七年级数学沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
20. (4分)若$(x^{2}-3x - 2)(x^{2}+px + q)展开后不含x^{3}和x^{2}$项,求$p$,$q$的值。
答案:
因为$ (x^{2} - 3x - 2)(x^{2} + px + q) = x^{4} + (p - 3)x^{3} + (q - 3p - 2) \cdot x^{2} - (3q + 2p)x - 2q $, 又因为乘积中不含$ x^{3} $与$ x^{2} $项,所以$ p - 3 = 0 $, $ q - 3p - 2 = 0 $, 所以$ p = 3 $, $ q = 11 $.
21. (6分)我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个等式。
例:如图①,可以得到$(a + b)(a + 2b)= a^{2}+3ab + 2b^{2}$。请解答下列问题:
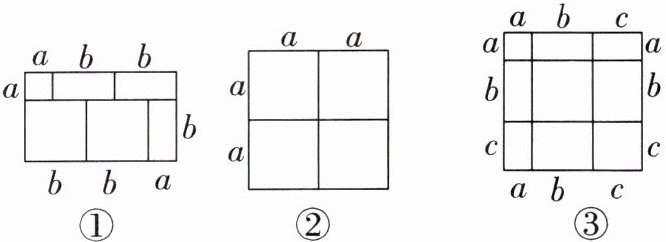
(1)根据图②,完成数学等式:$(2a)^{2}= $______
(2)观察图③,写出图③中所表示的等式;
(3)若$a = 7x - 5$,$b = -4x + 2$,$c = -3x + 4$,且$a^{2}+b^{2}+c^{2}= 37$,请利用(2)所得的结论求:$ab + bc + ac$的值。
例:如图①,可以得到$(a + b)(a + 2b)= a^{2}+3ab + 2b^{2}$。请解答下列问题:

(1)根据图②,完成数学等式:$(2a)^{2}= $______
$4a^{2}$
;(2)观察图③,写出图③中所表示的等式;
$(a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2ab + 2bc + 2ac$
(3)若$a = 7x - 5$,$b = -4x + 2$,$c = -3x + 4$,且$a^{2}+b^{2}+c^{2}= 37$,请利用(2)所得的结论求:$ab + bc + ac$的值。
$-18$
答案:
(1)$ 4a^{2} $
(2)$ (a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2ab + 2bc + 2ac $.
(3)因为$ a = 7x - 5 $, $ b = -4x + 2 $, $ c = -3x + 4 $, 所以$ a + b + c = 7x - 5 - 4x + 2 - 3x + 4 = 1 $. 因为$ (a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2ab + 2bc + 2ac $, 所以$ 1^{2} = 37 + 2(ab + ac + bc) $, 所以$ ab + ac + bc = -18 $.
(1)$ 4a^{2} $
(2)$ (a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2ab + 2bc + 2ac $.
(3)因为$ a = 7x - 5 $, $ b = -4x + 2 $, $ c = -3x + 4 $, 所以$ a + b + c = 7x - 5 - 4x + 2 - 3x + 4 = 1 $. 因为$ (a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2ab + 2bc + 2ac $, 所以$ 1^{2} = 37 + 2(ab + ac + bc) $, 所以$ ab + ac + bc = -18 $.
22. (8分)材料1:在一个含有两个字母的多项式中,如果任意交换两个字母的位置,多项式的值不变,则称这样的多项式为“二元轮换对称式”。例如$x^{2}+y^{2}$,$x^{3}+y^{3}$,$(5x - 3)(5y - 3)$,…都是“二元轮换对称式”,对于所有的“二元轮换对称式”都可以用含相同字母的另一个“二元轮换对称式”来表示,形成一个“基本轮换对称式”,例如:$x^{2}+y^{2}= (x + y)^{2}-2xy$是一个“基本轮换对称式”。
材料2:形如$x^{n}+y^{n}$($n≥2且n$为整数)的“基本轮换对称式”:
$x^{2}+y^{2}= (x + y)^{2}-2xy$
$x^{3}+y^{3}= (x^{2}+y^{2})(x + y)-xy(x + y)$
$x^{4}+y^{4}= (x^{3}+y^{3})(x + y)-xy(x^{2}+y^{2})$
…
通过阅读上列材料,解决以下问题。
(1)式子①$2a - 2b$;②$8a^{2}+3b^{2}$;③$a^{3}-2ab + b^{3}$;④$a^{3}+a^{2}b - ab^{2}+b^{3}$中,属于“二元轮换对称式”的是______(填序号)。
(2)根据材料2,直接写出$x^{n}+y^{n}$($n≥2且n$为整数)的“基本轮换对称式”。
(3)若已知$x + y = 7$,$xy = 3$,求$x^{3}+y^{3}$的值。
(4)若$x = 1 + a$,$y = 1 - a$,则$(x^{5}+y^{5})-2(x^{4}+y^{4})= $______(用含$a$的代数式表示)。
(1)
(2)$x^{n} + y^{n} = (x^{n - 1} + y^{n - 1})(x + y) - xy(x^{n - 2} + y^{n - 2})$
(3)280
(4)
材料2:形如$x^{n}+y^{n}$($n≥2且n$为整数)的“基本轮换对称式”:
$x^{2}+y^{2}= (x + y)^{2}-2xy$
$x^{3}+y^{3}= (x^{2}+y^{2})(x + y)-xy(x + y)$
$x^{4}+y^{4}= (x^{3}+y^{3})(x + y)-xy(x^{2}+y^{2})$
…
通过阅读上列材料,解决以下问题。
(1)式子①$2a - 2b$;②$8a^{2}+3b^{2}$;③$a^{3}-2ab + b^{3}$;④$a^{3}+a^{2}b - ab^{2}+b^{3}$中,属于“二元轮换对称式”的是______(填序号)。
(2)根据材料2,直接写出$x^{n}+y^{n}$($n≥2且n$为整数)的“基本轮换对称式”。
(3)若已知$x + y = 7$,$xy = 3$,求$x^{3}+y^{3}$的值。
(4)若$x = 1 + a$,$y = 1 - a$,则$(x^{5}+y^{5})-2(x^{4}+y^{4})= $______(用含$a$的代数式表示)。
(1)
③
(2)$x^{n} + y^{n} = (x^{n - 1} + y^{n - 1})(x + y) - xy(x^{n - 2} + y^{n - 2})$
(3)280
(4)
$6a^{4} - 4a^{2} - 2$
答案:
(1)③ 解析: ①当$ a $, $ b $不为0时,$ 2a - 2b \neq 2b - 2a $; ②$ 8a^{2} + 3b^{2} = 8b^{2} + 3a^{2} $不一定成立; ③$ a^{3} - 2ab + b^{3} = b^{3} - 2ab + a^{3} $; ④$ a^{3} + a^{2}b - ab^{2} + b^{3} = b^{3} + b^{2}a - ba^{2} + a^{3} $不一定成立. 综上可知,属于“二元轮换对称式”的是③. 故答案为③.
(2)形如$ x^{n} + y^{n} $($ n \geq 2 $且$ n $为整数)的“基本轮换对称式”:
$ x^{2} + y^{2} = (x + y)^{2} - 2xy $
$ x^{3} + y^{3} = (x^{2} + y^{2})(x + y) - xy(x + y) $
$ x^{4} + y^{4} = (x^{3} + y^{3})(x + y) - xy(x^{2} + y^{2}) $
...
所以$ x^{n} + y^{n} = (x^{n - 1} + y^{n - 1})(x + y) - xy(x^{n - 2} + y^{n - 2}) $,
即$ x^{n} + y^{n} $($ n \geq 2 $且$ n $为整数)的“基本轮换对称式”为$ x^{n} + y^{n} = (x^{n - 1} + y^{n - 1})(x + y) - xy(x^{n - 2} + y^{n - 2}) $.
(3)由题意可知,$ x^{3} + y^{3} = (x^{2} + y^{2})(x + y) - xy(x + y) $, 所以当$ x + y = 7 $, $ xy = 3 $时,
$ x^{3} + y^{3} = (x^{2} + y^{2})(x + y) - xy(x + y) = [(x + y)^{2} - 2xy](x + y) - xy(x + y) = (7^{2} - 2 × 3) × 7 - 3 × 7 = 280 $.
(4)$ 6a^{4} - 4a^{2} - 2 $ 解析: 因为$ x = 1 + a $, $ y = 1 - a $, 所以$ x + y = 2 $, $ xy = 1 - a^{2} $, 所以$ x^{5} + y^{5} = (x^{4} + y^{4})(x + y) - xy(x^{3} + y^{3}) = 2(x^{4} + y^{4}) - (1 - a^{2})(x^{3} + y^{3}) $, 所以$ (x^{5} + y^{5}) - 2(x^{4} + y^{4}) = -(1 - a^{2})(x^{3} + y^{3}) = -(1 - a^{2})[(x^{2} + y^{2})(x + y) - xy(x + y)] = -(1 - a^{2})[2(x^{2} + y^{2}) - 2(1 - a^{2})] $. 因为$ x^{2} + y^{2} = (x + y)^{2} - 2xy = 2^{2} - 2(1 - a^{2}) = 2 + 2a^{2} $, 所以$ (x^{5} + y^{5}) - 2(x^{4} + y^{4}) = -(1 - a^{2})[2(2 + 2a^{2}) - 2(1 - a^{2})] = -(1 - a^{2})(2 + 6a^{2}) = -2(1 - a^{2})(1 + 3a^{2}) = 6a^{4} - 4a^{2} - 2 $, 故答案为$ 6a^{4} - 4a^{2} - 2 $.
(1)③ 解析: ①当$ a $, $ b $不为0时,$ 2a - 2b \neq 2b - 2a $; ②$ 8a^{2} + 3b^{2} = 8b^{2} + 3a^{2} $不一定成立; ③$ a^{3} - 2ab + b^{3} = b^{3} - 2ab + a^{3} $; ④$ a^{3} + a^{2}b - ab^{2} + b^{3} = b^{3} + b^{2}a - ba^{2} + a^{3} $不一定成立. 综上可知,属于“二元轮换对称式”的是③. 故答案为③.
(2)形如$ x^{n} + y^{n} $($ n \geq 2 $且$ n $为整数)的“基本轮换对称式”:
$ x^{2} + y^{2} = (x + y)^{2} - 2xy $
$ x^{3} + y^{3} = (x^{2} + y^{2})(x + y) - xy(x + y) $
$ x^{4} + y^{4} = (x^{3} + y^{3})(x + y) - xy(x^{2} + y^{2}) $
...
所以$ x^{n} + y^{n} = (x^{n - 1} + y^{n - 1})(x + y) - xy(x^{n - 2} + y^{n - 2}) $,
即$ x^{n} + y^{n} $($ n \geq 2 $且$ n $为整数)的“基本轮换对称式”为$ x^{n} + y^{n} = (x^{n - 1} + y^{n - 1})(x + y) - xy(x^{n - 2} + y^{n - 2}) $.
(3)由题意可知,$ x^{3} + y^{3} = (x^{2} + y^{2})(x + y) - xy(x + y) $, 所以当$ x + y = 7 $, $ xy = 3 $时,
$ x^{3} + y^{3} = (x^{2} + y^{2})(x + y) - xy(x + y) = [(x + y)^{2} - 2xy](x + y) - xy(x + y) = (7^{2} - 2 × 3) × 7 - 3 × 7 = 280 $.
(4)$ 6a^{4} - 4a^{2} - 2 $ 解析: 因为$ x = 1 + a $, $ y = 1 - a $, 所以$ x + y = 2 $, $ xy = 1 - a^{2} $, 所以$ x^{5} + y^{5} = (x^{4} + y^{4})(x + y) - xy(x^{3} + y^{3}) = 2(x^{4} + y^{4}) - (1 - a^{2})(x^{3} + y^{3}) $, 所以$ (x^{5} + y^{5}) - 2(x^{4} + y^{4}) = -(1 - a^{2})(x^{3} + y^{3}) = -(1 - a^{2})[(x^{2} + y^{2})(x + y) - xy(x + y)] = -(1 - a^{2})[2(x^{2} + y^{2}) - 2(1 - a^{2})] $. 因为$ x^{2} + y^{2} = (x + y)^{2} - 2xy = 2^{2} - 2(1 - a^{2}) = 2 + 2a^{2} $, 所以$ (x^{5} + y^{5}) - 2(x^{4} + y^{4}) = -(1 - a^{2})[2(2 + 2a^{2}) - 2(1 - a^{2})] = -(1 - a^{2})(2 + 6a^{2}) = -2(1 - a^{2})(1 + 3a^{2}) = 6a^{4} - 4a^{2} - 2 $, 故答案为$ 6a^{4} - 4a^{2} - 2 $.
查看更多完整答案,请扫码查看


