《2025年暑假总动员宁夏人民教育出版社七年级数学沪科版》

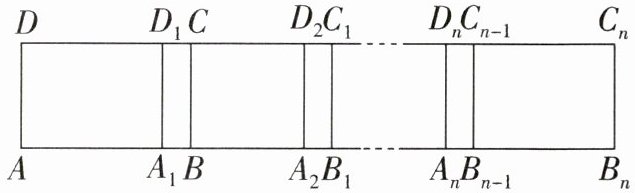
10. 如图,长方形$ABCD$中,$AB = 6$,第1次平移长方形$ABCD沿AB$的方向向右平移5个单位,得到长方形$A_{1}B_{1}C_{1}D_{1}$,第2次平移将长方形$A_{1}B_{1}C_{1}D_{1}沿A_{1}B_{1}$的方向向右平移5个单位,得到长方形$A_{2}B_{2}C_{2}D_{2}$……第$n次平移将长方形A_{n - 1}B_{n - 1}C_{n - 1}D_{n - 1}沿A_{n - 1}B_{n - 1}$的方向平移5个单位,得到长方形$A_{n}B_{n}C_{n}D_{n}(n ＞ 2)$,若$AB_{n}$的长度为2026,则$n$的值为(D)

A. 401
B. 402
C. 403
D. 404

答案： D

11. “$n$与4的差是负数”用不等式表示为$n - 4 ＜ 0$。

答案： $n - 4 ＜ 0$

12. 分式$\frac{1}{x^{2} - 3x}与\frac{2}{x^{2} - 9}$的最简公分母是$x ( x + 3 ) ( x - 3 )$。

答案： $x ( x + 3 ) ( x - 3 )$

13. 已知$x = 2$是不等式$(x - 5)(ax - 3a + 2)≤0$的解,且$x = 1$不是这个不等式的解,则实数$a$的取值范围是$1 ＜ a \leq 2$。

答案： $1 ＜ a \leq 2$

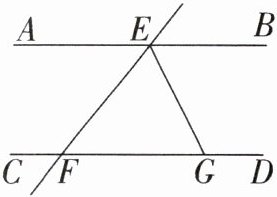
14. 如图,已知$AB// CD$,点$E$,$F在直线AB$,$CD$上,$EG平分∠BEF交CD于点G$,若$∠EGF = 64^{\circ}$,那么$∠AEF$的度数为______52°。

答案： $52 ^ { \circ }$

15. 若$3x^{3} - x = 1$,则$9x^{4} + 12x^{3} - 3x^{2} - 7x + 2025 = $2029。

答案： 2029

16. 如图为某正方形的房屋结构平面图,其中主卧与客卧都为正方形,其面积之和比其余面积(阴影部分)多2.25平方米,则主卧与客卧的周长差为______6米。

答案： 6

17. (4分)计算：$\sqrt{9} + (-1)^{2025}×(π - 3)^{0} - \sqrt[3]{27} + (\frac{1}{2})^{-2}$。

答案： 原式 $ = 3 + ( - 1 ) × 1 - 3 + 4 = 3$

18. (4分)先化简,再求值：$\frac{8a}{a^{2} + 4a + 4}÷\frac{a^{2} - 2a}{a^{2} - 4} - \frac{2}{a + 2}$,其中$a = (π - 3.14)^{0}$。

答案： 原式 $ = \frac { 8 a } { ( a + 2 ) ^ { 2 } } \cdot \frac { ( a + 2 ) ( a - 2 ) } { a ( a - 2 ) } - \frac { 2 } { a + 2 } = \frac { 8 } { a + 2 } - \frac { 2 } { a + 2 } = \frac { 6 } { a + 2 }$，当 $ a = ( \pi - 3.14 ) ^ { 0 } = 1$ 时，原式 $ = \frac { 6 } { 1 + 2 } = 2$

19. (8分)把下列各式因式分解：
(1)$m^{2}(a - b) + n^{2}(b - a)$；
(2)$2(a - 1)^{2} - 12(a - 1) + 18$；
(3)$x^{4} - 2x^{2} + 1$；
(4)$36x^{2}y^{2} - (9x^{2} + y^{2})^{2}$。

答案：
(1) $ ( a - b ) ( m + n ) ( m - n )$
(2) $ 2 ( a - 4 ) ^ { 2 }$
(3) $ ( x - 1 ) ^ { 2 } ( x + 1 ) ^ { 2 }$
(4) $ - ( 3 x - y ) ^ { 2 } ( 3 x + y ) ^ { 2 }$