《2025年暑假总动员宁夏人民教育出版社七年级数学沪科版》

9. 一个直棱柱有 12 个顶点,那么这个棱柱的底面是六边形。

答案： 六

10. 已知线段 $ AB = 10\ \text{cm} $,$ BC = 5\ \text{cm} $,$ A $,$ B $,$ C $ 三点在同一条直线上,则 $ AC = $5cm 或 15cm。

答案： 5cm 或 15cm

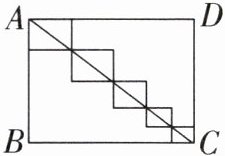
11. 如图,长方形 $ ABCD $ 的宽和长分别为 $ AB = 6 $,$ BC = 8 $,则图中五个小长方形的周长之和为28。

答案： 28

12. 如图,线段 $ AB $ 上有两点 $ M $,$ N $,点 $ M $ 分 $ AB $ 为 $ 1:2 $ 两部分,点 $ N $ 分 $ AB $ 为 $ 1:3 $ 两部分,若 $ MN = 2 $,则 $ AB $ 的长为______24。

答案： 24

13. 如图,已知 $ \angle A + \angle C = 180^\circ $,$ \angle APM = 118^\circ $,则 $ \angle CQN = $______62$^\circ $。

答案： 62

14. 若 $ \alpha $ 和 $ \beta $ 互补,且 $ \alpha ＞ \beta $,则下列表示 $ \beta $ 的余角的式子：① $ 90^\circ - \beta $；② $ \alpha - 90^\circ $；③ $ \frac{1}{2}(\alpha + \beta) $；④ $ \frac{1}{2}(\alpha - \beta) $。其中错误的有③(填写序号)。

答案： ③

15. 将一个含有 $ 45^\circ $ 角的直角三角板摆放在矩形上,如图所示,若 $ \angle 1 = 40^\circ $,则 $ \angle 2 = $______85$^\circ $。

答案： 85

16. 如图,将长方形 $ ABCD $ 折叠,折痕为 $ EF $,$ BC $ 的对应边 $ B'C' $ 与 $ CD $ 交于点 $ M $,若 $ \angle B'MD = 50^\circ $,则 $ \angle BEF $ 的度数为______70$^\circ $。

答案： 70 解析:因为$∠C'=∠C=90^{\circ },∠DMB'=∠C'MF=50^{\circ }$,所以$∠C'FM=40^{\circ }$,设$∠BEF=α$,则$∠EFC=180^{\circ }-α,∠DFE=∠BEF=α,∠C'FE=40^{\circ }+α$,由折叠可得,$∠EFC=∠EFC'$,所以$180^{\circ }-α=40^{\circ }+α$,所以$α=70^{\circ }$,所以$∠BEF=70^{\circ }$.

17. 如图,$ AB $ 段上有四处居民小区 $ A $,$ C $,$ D $,$ B $,且有 $ AC = CD = DB $,为改善居民的购物环境,想在 $ AB $ 上建一家超市(超市不建在小区内),每个小区的居民各执一词,难以定下具体的建设位置,高经理是超市负责人,从便民、获利的角度考虑,你觉得他会把超市建在哪儿？

线段 CD 上的某一处

答案： 若建在线段 CD 的某一点 E 处,设$CE=x,AC=a$,则四个小区居民到超市购物的总路程之和为$(a+x)+x+(a-x)+(2a-x)=4a$;若建在线段 AC 的某一点 F 处,设$CF=x,AC=a$,则四个小区居民到超市购物的总路程之和为$(a-x)+x+(a+x)+(2a+x)=4a+2x＞4a$.同样建在线段 DB 的某一点处，总路程之和也大于 4a,所以超市应建在线段 CD 上的某一处.