《2025年暑假总动员宁夏人民教育出版社七年级数学沪科版》

19. (4分)如图,已知C和D是线段AB上的两个点,且AB= a,CD= b(a＞b),M和N分别是AC和BD的中点,求MN的长。

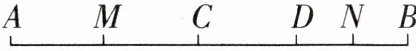
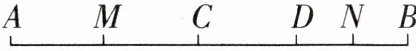
$\frac{1}{2}(a + b)$

答案： 因为 $MN = MC + CD + DN = MC + b + DN$, 而 $2MC + CD + 2DN = AB = a$, 所以 $MC + DN = \frac { 1 } { 2 } (a - b)$, 所以 $MN = b + \frac { 1 } { 2 } (a - b) = \frac { 1 } { 2 } (a + b)$.

20. (6分)如图,O为直线AB上一点,∠AOC= 45°,OD平分∠AOC,∠DOE= 90°。
(1)请你数一数,图中有多少个小于平角的角；9
(2)求出∠BOD的度数；157.5°
(3)请通过计算说明OE是否平分∠BOC。
因为∠BOE = 180° - ∠DOE - ∠AOD = 180° - 90° - 22.5° = 67.5°，∠COE = 90° - 22.5° = 67.5°，所以∠BOE = ∠COE，即OE平分∠BOC。

答案：
(1)题图中有 9 个小于平角的角.
(2)因为 OD 平分 $∠AOC$, $∠AOC = 45 ^ { \circ }$, 所以 $∠AOD = \frac { 1 } { 2 }×45 ^ { \circ } = 22.5 ^ { \circ }$, 所以 $∠BOD = 180 ^ { \circ } - 22.5 ^ { \circ } = 157.5 ^ { \circ }$.
(3)因为 $∠BOE = 180 ^ { \circ } - ∠DOE - ∠AOD = 180 ^ { \circ } - 90 ^ { \circ } - 22.5 ^ { \circ } = 67.5 ^ { \circ }$, $∠COE = 90 ^ { \circ } - 22.5 ^ { \circ } = 67.5 ^ { \circ }$, 所以 $∠BOE = ∠COE$, 即 OE 平分 $∠BOC$.

21. (6分)如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD= 10cm,设点B的运动时间为t秒(0≤t≤10)。
(1)当t= 2时。
①AB= ______4cm；
②求线段CD的长度。
(2)用含t的代数式表示运动过程中AB的长。
(3)在运动过程中,若AB的中点为E,则EC的长是否变化？若不变,求出EC的长；若发生变化,请说明理由。

答案：
(1)①4
②因为 $AD = 10 \mathrm {~cm}$, $AB = 4 \mathrm {~cm}$, 所以 $BD = 10 - 4 = 6 (\mathrm {~cm})$. 因为 C 是线段 BD 的中点, 所以 $CD = \frac { 1 } { 2 }BD = \frac { 1 } { 2 }×6 = 3 (\mathrm {~cm})$.
(2)因为 B 是线段 AD 上一动点, 沿 $A → D → A$ 以 $2 \mathrm {~cm}/\mathrm {s}$ 的速度往返运动 1 次, 所以当 $0 ≤ t ≤ 5$ 时, $AB = 2t \mathrm {~cm}$; 当 $5 ＜ t ≤ 10$ 时, $AB = 10 - (2t - 10) = 20 - 2t (\mathrm {~cm})$.
(3)不变. 因为 AB 的中点为 E,C 是线段 BD 的中点, 所以 $EC = \frac { 1 } { 2 }(AB + BD) = \frac { 1 } { 2 }AD = \frac { 1 } { 2 }×10 = 5 (\mathrm {~cm})$.