《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

13. 将多项式$4x^{2} + 4$加上一个单项式后,使它能成为另一个多项式的完全平方,添加的单项式可以是______。

答案： $ 8x $或$ -8x $或$ x^{4} $

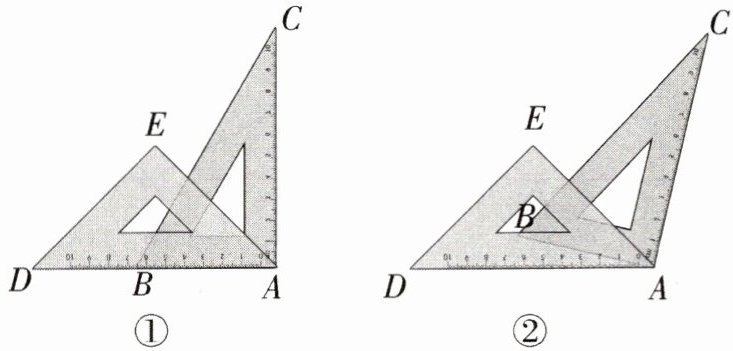
14. 一副直角三角尺叠放如图①所示,现将含$45^{\circ}角的三角尺ADE$固定不动,将含$30^{\circ}角的三角尺ABC绕顶点A$顺时针转动(旋转角不超过$180$度),使两块三角尺至少有一组边互相平行。如图②,当$∠BAD = 15^{\circ}$时,$BC// DE$。则$∠BAD(0^{\circ} ＜ ∠BAD ＜ 180^{\circ})$其他所有可能符合条件的度数为______。

答案： $ 45^{\circ}, 60^{\circ}, 105^{\circ}, 135^{\circ} $

15. 已知$∠AOB = 50^{\circ}$,$∠BOC与∠AOB$互为余角,求$∠AOC$的度数。

答案：
若 $ OB $ 在 $ \angle AOC $ 内部，如图①所示。因为 $ \angle BOC $ 与 $ \angle AOB $ 互为余角，则 $ \angle AOC = \angle AOB + \angle BOC = 90^{\circ} $。若 $ OB $ 在 $ \angle AOC $ 外部，如图②所示。因为 $ \angle BOC $ 与 $ \angle AOB $ 互为余角，则 $ \angle BOC = 90^{\circ} - \angle AOB = 90^{\circ} - 50^{\circ} = 40^{\circ} $，所以 $ \angle AOC = \angle AOB - \angle BOC = 50^{\circ} - 40^{\circ} = 10^{\circ} $。综上知 $ \angle AOC $ 等于 $ 90^{\circ} $或 $ 10^{\circ} $。
　　　　 　　

16. 解关于$x的方程(a - 2)x = b - 1$。

答案： 当 $ a - 2 \neq 0 $ 时，方程有唯一解 $ x = \frac{b - 1}{a - 2} $；
当 $ a - 2 = 0 $ 且 $ b - 1 = 0 $ 时，即 $ a = 2, b = 1 $ 时，方程有无数多个解；
当 $ a - 2 = 0 $ 且 $ b - 1 \neq 0 $ 时，即 $ a = 2, b \neq 1 $ 时，方程无解。

17. 如图,$P是线段AB$上任一点,$AB = 12\mathrm{cm}$,$C$,$D两点分别从P$,$B同时向A$点运动,且$C点的运动速度为2\mathrm{cm/s}$,$D点的运动速度为3\mathrm{cm/s}$,运动的时间为$t\mathrm{s}$。

(1)若$AP = 8\mathrm{cm}$,
①运动$1\mathrm{s}$后,求$CD$的长；
②当$D在线段PB$上运动时,试说明：$AC = 2CD$。
(2)如果$t = 2$时,$CD = 1\mathrm{cm}$,试探索$AP$的值。

答案：
(1) ①由题意可知，$ CP = 2 \times 1 = 2(cm) $，$ DB = 3 \times 1 = 3(cm) $。
因为 $ AP = 8cm $，$ AB = 12cm $，所以 $ PB = AB - AP = 4(cm) $，所以 $ CD = CP + PB - DB = 2 + 4 - 3 = 3(cm) $。
②因为 $ AP = 8cm $，$ AB = 12cm $，
所以 $ BP = 4cm $，$ AC = (8 - 2t)cm $，所以 $ DP = (4 - 3t)cm $，
所以 $ CD = CP + DP = 2t + 4 - 3t = (4 - t)cm $，所以 $ AC = 2CD $。
(2) 当 $ t = 2 $ 时，
$ CP = 2 \times 2 = 4(cm) $，$ DB = 3 \times 2 = 6(cm) $，
当点 $ D $ 在 $ C $ 的右边时，如图①所示：
由于 $ CD = 1cm $，
所以 $ CB = CD + DB = 7(cm) $，所以 $ AC = AB - CB = 5(cm) $，
所以 $ AP = AC + CP = 9(cm) $。
当点 $ D $ 在 $ C $ 的左边时，如图②所示：
所以 $ AD = AB - DB = 6(cm) $，
所以 $ AP = AD + CD + CP = 11(cm) $。
综上所述，$ AP = 9cm $或 $ 11cm $。

18. 阅读材料：
我们知道,现在我们可以来化简含有绝对值的代数式,如化简代数式$|x + 1| + |x - 2|$时,可令$x + 1 = 0和x - 2 = 0$,分别求得$x = -1$,$x = 2$(称$-1$,$2分别为|x + 1|与|x - 2|$的零点值)。在实数范围内,零点值$x = -1和x = 2可将全体实数分成不重复且不遗漏的如下3$种情况：①$x ＜ -1$；②$-1\leqslant x ＜ 2$；③$x\geqslant 2$。从而可将代数式$|x + 1| + |x - 2|化简为以下3$种情况：
(ⅰ)当$x ＜ -1$时,原式$= -(x + 1) - (x - 2) = -2x + 1$；
(ⅱ)当$-1\leqslant x ＜ 2$时,原式$= x + 1 - (x - 2) = 3$；
(ⅲ)当$x\geqslant 2$时,原式$= x + 1 + x - 2 = 2x - 1$。
综上讨论,原式$=\begin{cases}-2x + 1(x ＜ -1),\\3(-1\leqslant x ＜ 2),\\2x - 1(x\geqslant 2).\end{cases}$
通过以上阅读,请你解决以下问题：
(1)分别求出$|x + 2|和|x - 4|$的零点值；
(2)化简代数式$|x + 2| + |x - 4|$。

答案：
(1) $ |x + 2| $和$ |x - 4| $的零点值分别为 $ x = -2 $和 $ x = 4 $。
(2) 当 $ x ＜ -2 $ 时，原式 $ = -(x + 2) - (x - 4) = -2x + 2 $；
当 $ -2 \leq x ＜ 4 $ 时，原式 $ = x + 2 - (x - 4) = 6 $；
当 $ x \geq 4 $ 时，原式 $ = x + 2 + x - 4 = 2x - 2 $。
综上讨论，原式 $ = \begin{cases} -2x + 2(x ＜ -2), \\ 6(-2 \leq x ＜ 4), \\ 2x - 2(x \geq 4). \end{cases} $