《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

21. 如图,数轴上点 A,B 表示的有理数分别为-6,3,点 P 是射线 AB 上一个动点(不与点 A,B 重合).M 是线段 AP 靠近点 A 的三等分点,N 是线段 BP 靠近点 B 的三等分点.
(1)若点 P 表示的有理数是 0,那么 MN 的长为______;若点 P 表示的有理数是 6,那么 MN 的长为______.
(2)点 P 在射线 AB 上运动(不与点 A,B 重合)的过程中,MN 的长是否发生改变?若不改变,请写出求 MN 的长的过程;若改变,请说明理由.

答案：

(1)6　6解析:若点P表示的有理数是0(如图①)，则AP=6,BP=3.因为M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点，所以MP=$\frac{2}{3}$AP=4,NP=$\frac{2}{3}$BP=2,所以MN=MP+NP=6;若点P表示的有理数是6(如图②),则AP=12,BP=3.因为M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点，所以MP=$\frac{2}{3}$AP=8,NP=$\frac{2}{3}$BP=2,所以MN=MP−NP=6.
(2)MN的长不会发生改变.设点P表示的有理数是a.当点P在点A,B之间时(如图①),AP=a+6,BP=3−a.因为M是线段AP靠近点A的三等分点，N是线段BP靠近点B的三等分点，所以MP=$\frac{2}{3}$AP=$\frac{2}{3}$(a+6),NP=$\frac{2}{3}$BP=$\frac{2}{3}$(3−a),所以MN=MP+NP=6;当点P在点B右侧时(如图②),AP=a+6,BP=a−3.因为M是线段AP靠近点A的三等分点，N是线段BP靠近点B的三等分点，所以MP=$\frac{2}{3}$AP=$\frac{2}{3}$(a+6),NP=$\frac{2}{3}$BP=$\frac{2}{3}$(a−3),所以MN=MP−NP=6.综上所述，点P在射线AB上运动(不与点A,B重合)的过程中,MN的长为定值6.

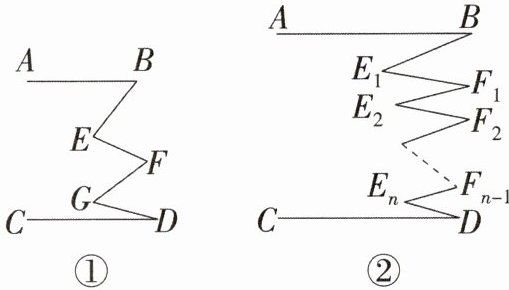
22. (1)在图①中,若$AB// CD,∠E+∠G与∠B+∠F+∠D$之间有什么数量关系? 请证明你的结论.
(2)在图②中,若$AB// CD$,又得到什么结论? (直接写出你的结论)

答案：
(1)∠E+∠G=∠B+∠F+∠D.证明:过点E向右作EM//AB,过点F向左作FN//AB，过点G向右作GH//AB.因为AB//CD,所以AB//EM//FN//GH//CD,所以∠B=∠BEM,∠MEF=∠EFN,∠NFG=∠FGH,∠HGD=∠D,所以∠BEF+∠FGD=∠BEM+∠MEF+∠FGH+∠HGD=∠B+∠EFN+∠NFG+∠D=∠B+∠EFG+∠D,即∠E+∠G=∠B+∠F+∠D.
(2)∠E₁+∠E₂+...+∠Eₙ=∠B+∠F₁+∠F₂+...+∠Fₙ₋₁+∠D.