《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

21. (10分)有$A,B$两家店,销售同样品质的商品,零售价都为20元/千克。$A$店规定：购买数量不超过100千克,全部按零售价的90%优惠；购买数量超过100千克但不超过200千克,全部按零售价的80%优惠；超过200千克的,全部按零售价的70%优惠。$B$店的规定如表：

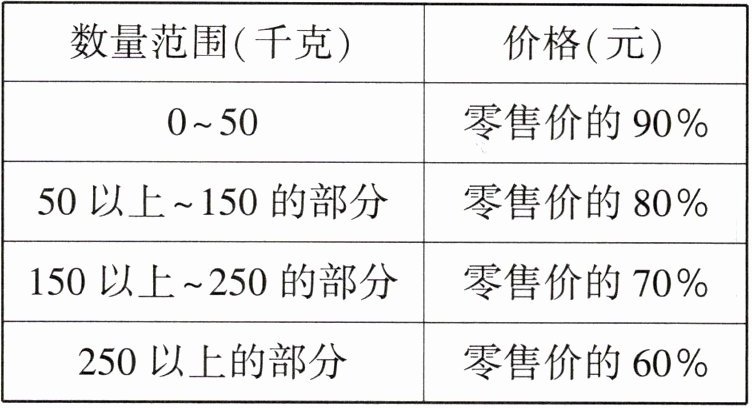
(1)如果在$A,B$两家店分别购买该商品60千克,共需要多少元？
(2)如果购买该商品$x$千克($150＜x＜200$),请你分别用含$x的代数式表示在A,B$两家店购买所需的费用。
(3)若要购买该商品180千克,选择在哪家店购买更优惠,请说明理由。

答案：
(1) 由题意可得，A 店: $ 60×20×90\% = 1080 $ (元)，
B 店: $ 50×20×90\% + 20×(60 - 50)×80\% = 1060 $ (元)。
$ 1080 + 1060 = 2140 $ (元)。
答:在 A，B 两家店分别购买该商品 60 千克，共需要 2140 元。
(2) 由题意可得，A 店: $ 20x×80\% = 16x $ (元)。
B 店: $ 50×20×90\% + 100×20×80\% + (x - 150)×20×70\% = (14x + 400) $ (元)。
答:在 A 店购买需要 $ 16x $ 元，在 B 店购买需要 $ (14x + 400) $ 元。
(3) 选择 A 店购买更优惠，理由:
由题意可得，在 A 店花费为 $ 16x = 16×180 = 2880 $ (元)，
在 B 店花费为 $ 14x + 400 = 14×180 + 400 = 2920 $ (元)。
因为 $ 2880 ＜ 2920 $，所以选择在 A 店购买更优惠。

22. (10分)如图①所示是一个长为$2m$、宽为$2n$的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形。

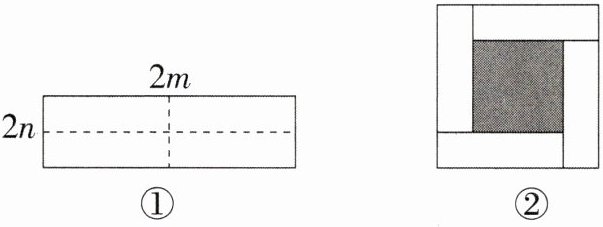
(1)你认为图②中的阴影部分的正方形的边长等于____。
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积。
方法①____；
方法②____。
(3)观察图①②,你能写出$(m+n)^{2},(m-n)^{2},mn$这三个代数式之间的等量关系吗？
(4)根据第(3)题中的等量关系,解决下列问题：若$a+b= 3,ab= 2$,则求$(a-b)^{2}$。

答案：
(1) $ m - n $
(2) $ (m + n)^2 - 4mn $ $ (m - n)^2 $
(3) $ (m + n)^2 - 4mn = (m - n)^2 $。
(4) $ (a - b)^2 = (a + b)^2 - 4ab $。
因为 $ a + b = 3 $，$ ab = 2 $，所以 $ (a - b)^2 = 9 - 8 = 1 $。