第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 按一定规律排列的单项式:$x,3x^{2},5x^{3},7x^{4},9x^{5},... $,第$n$个单项式是()
A. $(2n - 1)x^{n}$
B. $(2n + 1)x^{n}$
C. $(n - 1)x^{n}$
D. $(n + 1)x^{n}$
A. $(2n - 1)x^{n}$
B. $(2n + 1)x^{n}$
C. $(n - 1)x^{n}$
D. $(n + 1)x^{n}$
答案:
A
2. 观察图中的“品”字形中数字之间的规律,根据观察到的规律得出$a$的值为()
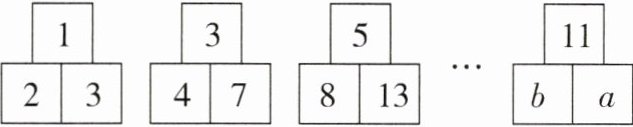
A. 75
B. 89
C. 103
D. 139

A. 75
B. 89
C. 103
D. 139
答案:
A
3. 如图,有一些用点组成形如四边形的图案,每条“边”(包括顶点)有$n(n>1)$个点.当$n = 100$时,这个图形总的点数$S$为()
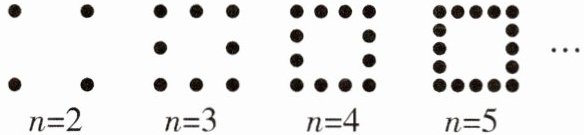
A. 396
B. 400
C. 404
D. 408
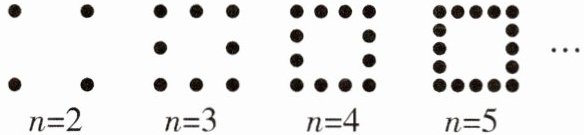
A. 396
B. 400
C. 404
D. 408
答案:
A
4. 如图所示是搭火柴棒游戏,用$x$表示所搭正方形的个数,那么搭$x$个这样的正方形需要多少根火柴棒?以下是几位同学的不同解法,他们为此争论不休,你能判断出谁对谁错吗?
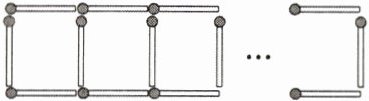
①小华说:“如果把最左边的那根拿掉,那么每个正方形恰好用了3根,所以共需$(3x + 1)$根火柴棒.”
②小明说:“外面的长方形共用了$(2x + 2)$根,中间还有$(x - 1)$根,所以共需$[(2x + 2)+(x - 1)]$根火柴棒.”
③小高说:“第一个正方形用4根,每增加一个正方形就会增加3根,所以共需$[4 + 3(x - 1)]$根火柴棒.”
④小平说:“上、下两排共用了$2x$根,竖直方向共用了$(x + 1)$根,所以共需$[2x+(x + 1)]$根火柴棒.”
⑤小亮说:“搭一个正方形需4根,搭$x个正方形需4x$根,但重复了$(x - 1)$根,所以共需$[4x-(x - 1)]$根火柴棒.”
上述解法中正确的个数是()
A. 2
B. 3
C. 4
D. 5

①小华说:“如果把最左边的那根拿掉,那么每个正方形恰好用了3根,所以共需$(3x + 1)$根火柴棒.”
②小明说:“外面的长方形共用了$(2x + 2)$根,中间还有$(x - 1)$根,所以共需$[(2x + 2)+(x - 1)]$根火柴棒.”
③小高说:“第一个正方形用4根,每增加一个正方形就会增加3根,所以共需$[4 + 3(x - 1)]$根火柴棒.”
④小平说:“上、下两排共用了$2x$根,竖直方向共用了$(x + 1)$根,所以共需$[2x+(x + 1)]$根火柴棒.”
⑤小亮说:“搭一个正方形需4根,搭$x个正方形需4x$根,但重复了$(x - 1)$根,所以共需$[4x-(x - 1)]$根火柴棒.”
上述解法中正确的个数是()
A. 2
B. 3
C. 4
D. 5
答案:
D
5. 如图是蜘蛛结网过程示意图,一只蜘蛛先以$O为起点结六条线OA,OB,OC,OD,OE,OF$后,再从线$OA上某点开始按逆时针方向依次在OA,OB,OC,OD,OE,OF,OA,…$上结网,若将各线上的结点依次记为$1,2,3,4,5,6,7,…$,则第1000个结点在()
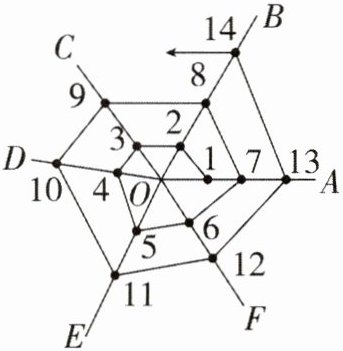
A. 线$OA$上
B. 线$OB$上
C. 线$OD$上
D. 线$OE$上

A. 线$OA$上
B. 线$OB$上
C. 线$OD$上
D. 线$OE$上
答案:
C
查看更多完整答案,请扫码查看


