《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

12. 若点 $A$,$B$ 在数轴上表示的数分别是 $a$,$b$,且 $|a| = 3$,$|b| = 1$,则 $A$,$B$ 两点之间的距离为______.

答案： 2 或 4

13. 若规定 $[a]$ 表示不超过 $a$ 的最大整数,例如 $[4.3]= 4$,若 $m = [\pi + 1]$,$n = [2.1]$,则 $[m+\frac{9}{4}n]$ 在此规定下的值为______.

答案： 8

14. 读一读：式子“$1 + 2 + 3 + 4 + … + 100$”表示从 1 开始的 100 个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将

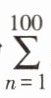
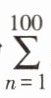
其表示为 $\sum_{n = 1}^{100}n$,这里“$\sum$”是求和符号,通过对以上材料的阅读,计算 $\sum_{n = 1}^{2000}\frac{1}{n(n + 1)}= $______.

答案： $\frac{2000}{2001}$

15. 某计算程序如图所示,当输入 $x= $______时,输出的 $y = 3$.

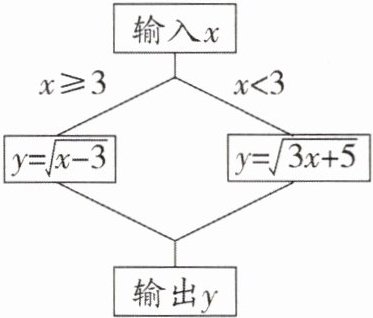
答案： 12 或 $\frac{4}{3}$

16. 多项式 $6x^{3}-11x^{2}+x + 4$ 可分解为______.

答案： $(x - 1)(3x - 4)(2x + 1)$

17. 计算和化简：
(1)计算：$\sqrt{16}+\sqrt[3]{-27}-|1-\sqrt{2}|$；
(2)实数 $a$,$b$ 在数轴上对应点的位置如图所示.化简：$\sqrt{a^{2}}-\sqrt{(a + b)^{2}}+|b - 2|$.

答案：
(1) 原式 $= 4 - 3 - (\sqrt{2} - 1) = 1 - \sqrt{2} + 1 = 2 - \sqrt{2}$。
(2) 由数轴可知：$a ＜ 0$，$a + b ＜ 0$，$b - 2 ＜ 0$，所以 $\sqrt{a^{2}} - \sqrt{(a + b)^{2}} + |b - 2| = |a| - |a + b| + |b - 2| = -a + a + b + 2 - b = 2$。

1

8. 先化简,再求值：$(1-\frac{4}{a + 2})÷\frac{a^{2}-4a + 4}{2a - 4}$,其中 $a = 2^{-1}+(\pi - 1000)^{0}$.

答案： 原式 $= (\frac{a + 2}{a + 2} - \frac{4}{a + 2}) \div \frac{(a - 2)^{2}}{2(a - 2)}$
$= \frac{a - 2}{a + 2} \cdot \frac{2}{a - 2} = \frac{2}{a + 2}$，
当 $a = 2^{-1} + (\pi - 1000)^{0} = \frac{1}{2} + 1 = \frac{3}{2}$ 时，
原式 $= \frac{2}{\frac{3}{2} + 2} = \frac{2}{\frac{7}{2}} = \frac{4}{7}$。

19. 阅读下列材料：
对于多项式 $x^{2}+x - 2$,如果我们把 $x = 1$ 代入此多项式,发现 $x^{2}+x - 2$ 的值为 0,这时可以确定多项式中有因式 $(x - 1)$；同理,可以确定多项式中有另一个因式 $(x + 2)$,于是我们可以得到 $x^{2}+x - 2= (x - 1)(x + 2)$.
又如：对于多项式 $2x^{2}-3x - 2$,发现当 $x = 2$ 时,$2x^{2}-3x - 2$ 的值为 0,则多项式 $2x^{2}-3x - 2$ 有一个因式 $(x - 2)$,我们可以设 $2x^{2}-3x - 2= (x - 2)(mx + n)$,解得 $m = 2$,$n = 1$,于是我们可以得到 $2x^{2}-3x - 2= (x - 2)(2x + 1)$.
请你根据以上材料,解答以下问题：
(1)当 $x = 1$ 时,多项式 $6x^{2}-x - 5$ 的值为 0,所以多项式 $6x^{2}-x - 5$ 有因式______,从而因式分解 $6x^{2}-x - 5= $______；
(2)以上这种因式分解的方法叫试根法,常用来分解一些比较复杂的多项式,请你尝试用试根法分解多项式：$2x^{2}+5x + 3$.

答案：
(1) $x - 1$ $(x - 1)(6x + 5)$ 解析：当 $x = 1$ 时，$6x^{2} - x - 5 = 0$，设 $6x^{2} - x - 5 = (x - 1)(mx + n)$，解得 $m = 6$，$n = 5$，所以因式分解 $6x^{2} - x - 5 = (x - 1)(6x + 5)$。
(2) 当 $x = -1$ 时，$2x^{2} + 5x + 3 = 0$，设 $2x^{2} + 5x + 3 = (x + 1) \cdot (mx + n)$，解得 $m = 2$，$n = 3$，所以 $2x^{2} + 5x + 3 = (x + 1) \cdot (2x + 3)$。