《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

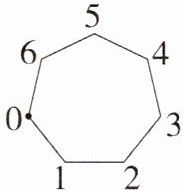
6. 如图,一枚棋子放在七角棋盘的第0号角上,现依逆时针方向移动这枚棋子,其各步依次移动$1,2,3,…,n$个角,如第一步从第0号角移动到第1号角,第二步从第1号角移动到第3号角,第三步从第3号角移动到第6号角……$$若这枚棋子不停地移动下去,则这枚棋子永远不能到达的角的个数是()

A. 0
B. 1
C. 2
D. 3

答案： D

7. 如图,房间地面的图案是用大小相同的黑、白正方形镶嵌而成,其中,第1个黑色“L”形由3个正方形组成,第2个黑色“L”形由7个正方形组成……$$那么第5个黑色“L”形的正方形个数是______.

答案： 19

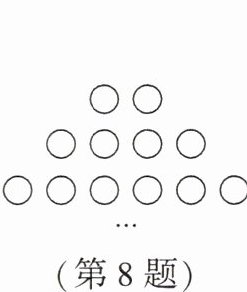
8. 将一些圆按照如图方式摆放,从上向下有无数行,其中第一行有2个圆,第二行有4个圆,第三行有6个圆……$$按此规律摆放下去,则前50行共有圆______个.

答案： 2550

9. 已知：$3^{1}= 3,3^{2}= 9,3^{3}= 27,3^{4}= 81,3^{5}= 243,3^{6}= 729,…$,设$A = 2(3 + 1)(3^{2}+1)(3^{4}+1)\cdot(3^{8}+1)(3^{16}+1)(3^{32}+1)+1$,则$A$的个位数字是______.

答案： 1

10. 已知$a_{1}= \frac{t}{1 + t},a_{2}= \frac{1}{1 - a_{1}},a_{3}= \frac{1}{1 - a_{2}},…,a_{n + 1}= \frac{1}{1 - a_{n}}$($n$为正整数,且$t\neq0,-1$),则$a_{2040}= $______(用含有$t$的代数式表示).

答案： $-\frac{1}{t}$

11. 如图,将一张正方形纸片剪成四个小正方形,称为第一次操作；然后将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作；再将其中的一个正方形剪成四个小正方形,共得到10个小正方形,称为第三次操作,…$$.根据以上操作,若要得到2233个小正方形,则需要操作的次数是______.(小正方形均为由单个的正方形组成)

答案： 744

12. 砸“金蛋”游戏：把210个“金蛋”连续编号为$1,2,3,…,210$,接着把编号是3的整数倍的“金蛋”全部砸碎；然后将剩下的“金蛋”重新连续编号为$1,2,3,…$,接着把编号是3的整数倍的“金蛋”全部砸碎……$$按照这样的方法操作,直到无编号是3的整数倍的“金蛋”为止.操作过程中砸碎编号是“66”的“金蛋”共______个.

答案： 3

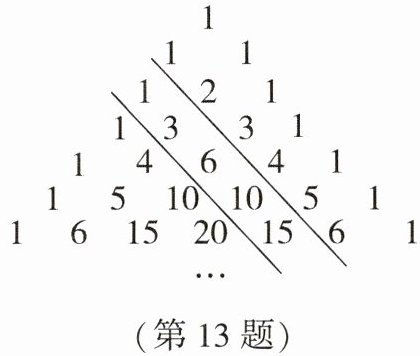
13. 如图被称为“杨辉三角”.其规律是：从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和.表中两平行线之间的一列数是：$1,3,6,10,15,…$,我们把第一个数记为$a_{1}$,第二个数记为$a_{2}$,第三个数记为$a_{3},…$,第$n个数记为a_{n}$,则$a_{4}+a_{200}= $______.

答案： 20110