《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

24. (12分)为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组。在环保局工作人员的帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位：dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下：

根据表中提供的信息解答下列问题：
(1)表中的c值为______；
(2)补全频数直方图；
(3)如果全市共有200个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个？

答案：
(1) 0.3
(2) $a = 40×0.2 = 8$，$b = 40 - 4 - 8 - 10 - 6 = 12$。图略。
(3) 由样本估计总体得 $200×(0.1 + 0.2) = 60$（个）。
答：在这一时刻噪声声级小于 75 dB 的测量点约有 60 个。

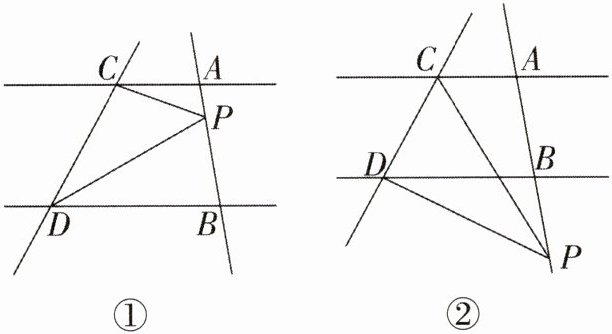
25. (14分)如图,已知直线$AC// BD$,直线AB,CD不平行,点P在直线AB上,且和点A,B不重合。
(1)如图①,当点P在线段AB上时,若$∠PCA= 20^{\circ}$,$∠PDB= 30^{\circ}$,求$∠CPD$的度数。
(2)当点P在A,B两点之间运动时,$∠PCA$,$∠PDB$,$∠CPD$之间满足什么样的等量关系？(直接写出答案)
(3)如图②,当点P在线段AB延长线上运动时,$∠PCA$,$∠PDB$,$∠CPD$之间满足什么样的等量关系？并说明理由。

答案：

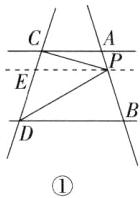
(1) 如图①，过 P 点作 $PE // AC$ 交 CD 于 E 点，则 $∠CPE = ∠PCA = 20^{\circ}$。因为 $AC // BD$，所以 $PE // BD$，所以 $∠DPE = ∠PDB = 30^{\circ}$，所以 $∠CPD = ∠CPE + ∠DPE = 50^{\circ}$。
(2) $∠CPD = ∠PCA + ∠PDB$。
(3) $∠CPD = ∠PCA - ∠PDB$。理由如下：
如图②，过 P 点作 $PF // BD$ 交 CD 于 F 点，则 $∠DPF = ∠PDB$。
因为 $AC // BD$，所以 $PF // AC$，
所以 $∠CPF = ∠PCA$，
所以 $∠CPD = ∠CPF - ∠DPF = ∠PCA - ∠PDB$。