《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

23. (14分)某商场经销A、B两种商品,A种商品每件售价60元,利润率为50%,B种商品每件进价50元,售价80元.
(1)A种商品每件进价为____元,B种商品每件利润率为____；
(2)若该商场同时购进A、B两种商品共50件,恰好总进价为2 100元,求购进A、B两种商品各多少件；
(3)在“春节”期间,该商场只对A、B两种商品进行如下的优惠促销活动：

按上述优惠条件,若小华一次性购买A、B商品实际付款522元,求若没有优惠促销,小华在该商场购买同样商品要付多少元.

答案：
(1)40 60% 解析:设A种商品每件进价m元,A种商品每件售价60元,利润率为50%,根据题意得60 - m = m×50%,解得m = 40,设B种商品每件利润率为n,B种商品每件进价50元,售价80元.根据题意得80 - 50 = 50n,解得n = $\frac{30}{50}$×100% = 60%.
(2)设购进A种商品x件,则购进B种商品(50 - x)件,根据题意,得40x + 50(50 - x) = 2100,
解得x = 40.所以50 - x = 50 - 40 = 10.
答:购进A种商品40件,B种商品10件.
(3)设小华打折前应付款为y元,
①打折前购物金额多于450元,但少于600元,
根据题意,得0.9y = 522,
解得y = 580;
②打折前购物金额不少于600元,
600×0.8 + (y - 600)×0.7 = 522,
解得y = 660.
答:小华在该商场购买同样商品要付580元或660元.

24. (14分)如图①,O为直线AB上一点,过点O作射线OC,使$∠BOC= 120^{\circ }$.将一直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
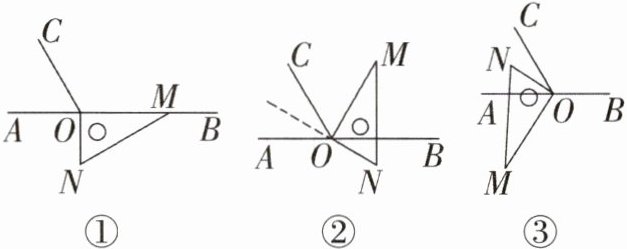
(1)将图①中的三角尺绕点O逆时针旋转至图②,使一边OM在$∠BOC$的内部,且恰好平分$∠BOC$.问：此时直线ON是否平分$∠AOC$？并说明理由.
(2)将图①中的三角尺绕点O以每秒$6^{\circ }$的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角$∠AOC$,求t的值.
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在$∠AOC$的内部,试探索：在旋转过程中,$∠AOM与∠NOC$的差是否发生变化？若不变,请求出这个差值；若变化,请求出差的变化范围.

答案：

(1)直线ON平分∠AOC.
理由:如图所示,设ON的反向延长线为OD.

因为OM平分∠BOC,所以∠MOC = ∠MOB.
又因为OM⊥ON,所以∠MOD = ∠MON = 90°.
所以∠COD = ∠BON.
又因为∠AOD = ∠BON(对顶角相等),
所以∠COD = ∠AOD.
所以OD平分∠AOC,即直线ON平分∠AOC.
(2)当直线ON恰好平分锐角∠AOC时,设ON的反向延长线为OD.
因为∠BOC = 120°,所以∠AOC = 60°.
所以∠BON = ∠COD = 30°.
即旋转60°或240°时,直线ON恰好平分锐角∠AOC.
由题意得,6t = 60或240.解得t = 10或40.
(3)∠AOM与∠NOC的差不变.
因为∠MON = 90°,∠AOC = 60°,
所以∠AOM = 90° - ∠AON,∠NOC = 60° - ∠AON.
所以∠AOM - ∠NOC = (90° - ∠AON) - (60° - ∠AON) = 30°.