第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
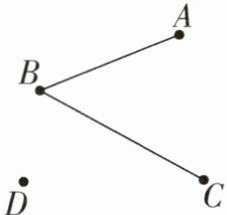
20. (8分)如图,已知平面内有线段AB,BC和点D,且AB<BC,请按下列要求作图.
(1)作射线AB,并在射线AB上取点E,使得BE= BC(请用无刻度的直尺和圆规作图,并保留作图痕迹,不写作法);
(2)在BC上取一点F,使得AF+DF最短,并说明理由.
(1)作射线AB,并在射线AB上取点E,使得BE= BC(请用无刻度的直尺和圆规作图,并保留作图痕迹,不写作法);
(2)在BC上取一点F,使得AF+DF最短,并说明理由.

答案:
(1)如图,延长线段 $AB$.以点 $B$ 为圆心, $BC$ 的长为半径画弧,交 $AB$ 的延长线于点 $E$,则点 $E$ 即为所求.

(2)如图,连结 $AD$ 交 $BC$ 于点 $F$,则点 $F$ 即为所求.
理由:两点之间线段最短.
(1)如图,延长线段 $AB$.以点 $B$ 为圆心, $BC$ 的长为半径画弧,交 $AB$ 的延长线于点 $E$,则点 $E$ 即为所求.

(2)如图,连结 $AD$ 交 $BC$ 于点 $F$,则点 $F$ 即为所求.
理由:两点之间线段最短.
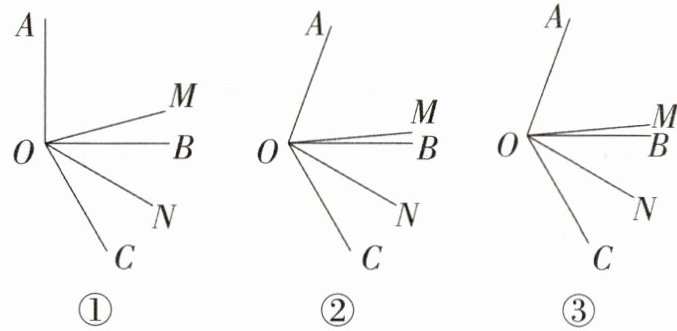
21. (10分)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图①,当∠AOB= 90°,∠BOC= 60°时,∠MON的度数是多少?为什么?
(2)如图②,当∠AOB= 70°,∠BOC= 60°时,∠MON= ______(直接写出结果).
(3)如图③,当∠AOB= α,∠BOC= β时,猜想:∠MON= ______(直接写出结果).
(1)如图①,当∠AOB= 90°,∠BOC= 60°时,∠MON的度数是多少?为什么?
(2)如图②,当∠AOB= 70°,∠BOC= 60°时,∠MON= ______(直接写出结果).
(3)如图③,当∠AOB= α,∠BOC= β时,猜想:∠MON= ______(直接写出结果).

答案:
(1) $∠MON = 45^{\circ}$.理由:因为 $∠AOB = 90^{\circ}$, $∠BOC = 60^{\circ}$,所以 $∠AOC = 90^{\circ} + 60^{\circ} = 150^{\circ}$.
因为 $OM$ 平分 $∠AOC$, $ON$ 平分 $∠BOC$,
所以 $∠MOC = \frac{1}{2}∠AOC = 75^{\circ}$, $∠NOC = \frac{1}{2}∠BOC = 30^{\circ}$,
所以 $∠MON = ∠MOC - ∠NOC = 45^{\circ}$.
(2) $35^{\circ}$
(3) $\frac{1}{2}\alpha$
(1) $∠MON = 45^{\circ}$.理由:因为 $∠AOB = 90^{\circ}$, $∠BOC = 60^{\circ}$,所以 $∠AOC = 90^{\circ} + 60^{\circ} = 150^{\circ}$.
因为 $OM$ 平分 $∠AOC$, $ON$ 平分 $∠BOC$,
所以 $∠MOC = \frac{1}{2}∠AOC = 75^{\circ}$, $∠NOC = \frac{1}{2}∠BOC = 30^{\circ}$,
所以 $∠MON = ∠MOC - ∠NOC = 45^{\circ}$.
(2) $35^{\circ}$
(3) $\frac{1}{2}\alpha$
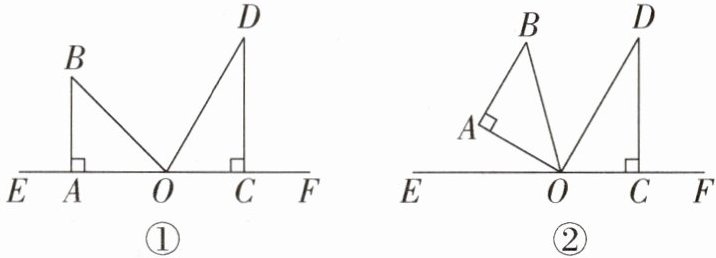
22. (10分)(1)如图①,把一副三角尺拼接在一
起,其中OA,OC与直线EF重合,∠AOB= 45°,∠COD= 60°,则∠BOD的度数为______;
(2)如图②,三角尺COD固定不动,将三角尺AOB绕着点O以每秒4°的速度按顺时针方向旋转.在旋转过程中,两块三角尺都在直线EF的上方.设三角尺AOB的旋转时间为t秒,在旋转过程中,当OB平分∠AOD时,求出时间t的值;
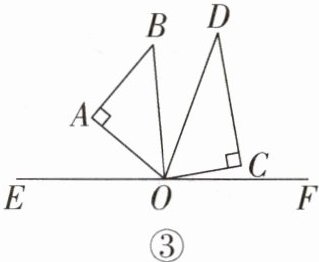
(3)如图③,若三角尺AOB绕着点O以每秒4°的速度按顺时针方向旋转的同时,三角尺COD同时也绕着点O以每秒1°的速度按逆时针方向旋转,在旋转过程中,两块三角尺都在直线EF的上方.当三角尺AOB停止旋转时,三角尺COD也停止旋转.设三角尺AOB的旋转时间为t秒,在旋转过程中,是否存在某一时刻使∠BOC= 2∠AOD?若存在,求出t的值;若不存在,请说明理由.

起,其中OA,OC与直线EF重合,∠AOB= 45°,∠COD= 60°,则∠BOD的度数为______;
(2)如图②,三角尺COD固定不动,将三角尺AOB绕着点O以每秒4°的速度按顺时针方向旋转.在旋转过程中,两块三角尺都在直线EF的上方.设三角尺AOB的旋转时间为t秒,在旋转过程中,当OB平分∠AOD时,求出时间t的值;
(3)如图③,若三角尺AOB绕着点O以每秒4°的速度按顺时针方向旋转的同时,三角尺COD同时也绕着点O以每秒1°的速度按逆时针方向旋转,在旋转过程中,两块三角尺都在直线EF的上方.当三角尺AOB停止旋转时,三角尺COD也停止旋转.设三角尺AOB的旋转时间为t秒,在旋转过程中,是否存在某一时刻使∠BOC= 2∠AOD?若存在,求出t的值;若不存在,请说明理由.

答案:
(1) $75^{\circ}$
(2)当 $OB$ 平分 $∠AOD$ 时,
因为 $∠AOB = 45^{\circ}$,
所以 $∠AOB = ∠BOD = 45^{\circ}$,
所以旋转角为 $75^{\circ} - 45^{\circ} = 30^{\circ}$,
所以 $t = 30÷4 = \frac{15}{2}$
(3)存在,理由:
当 $OA$ 在 $OD$ 左侧时,如图①,

根据旋转可知 $∠AOD = 180^{\circ} - 60^{\circ} - (4 + 1)^{\circ}t = 120^{\circ} - 5^{\circ}t$,
$∠BOC = 180^{\circ} - 45^{\circ} - (4 + 1)^{\circ}t = 135^{\circ} - 5^{\circ}t$.
因为 $∠BOC = 2∠AOD$,
所以 $135^{\circ} - 5^{\circ}t = 2(120^{\circ} - 5^{\circ}t)$,
解得 $t = 21$;
当 $OA$ 在 $OD$ 右侧时,如图②,

$∠AOD = 5^{\circ}t + 60^{\circ} - 180^{\circ} = 5^{\circ}t - 120^{\circ}$,
$∠BOC = 180^{\circ} - 45^{\circ} - (4 + 1)^{\circ}t = 135^{\circ} - 5^{\circ}t$.
因为 $∠BOC = 2∠AOD$,
所以 $135^{\circ} - 5^{\circ}t = 2(5^{\circ}t - 120^{\circ})$,
所以 $t = 25$.
综上, $t$ 的值为21或25.
(1) $75^{\circ}$
(2)当 $OB$ 平分 $∠AOD$ 时,
因为 $∠AOB = 45^{\circ}$,
所以 $∠AOB = ∠BOD = 45^{\circ}$,
所以旋转角为 $75^{\circ} - 45^{\circ} = 30^{\circ}$,
所以 $t = 30÷4 = \frac{15}{2}$
(3)存在,理由:
当 $OA$ 在 $OD$ 左侧时,如图①,

根据旋转可知 $∠AOD = 180^{\circ} - 60^{\circ} - (4 + 1)^{\circ}t = 120^{\circ} - 5^{\circ}t$,
$∠BOC = 180^{\circ} - 45^{\circ} - (4 + 1)^{\circ}t = 135^{\circ} - 5^{\circ}t$.
因为 $∠BOC = 2∠AOD$,
所以 $135^{\circ} - 5^{\circ}t = 2(120^{\circ} - 5^{\circ}t)$,
解得 $t = 21$;
当 $OA$ 在 $OD$ 右侧时,如图②,

$∠AOD = 5^{\circ}t + 60^{\circ} - 180^{\circ} = 5^{\circ}t - 120^{\circ}$,
$∠BOC = 180^{\circ} - 45^{\circ} - (4 + 1)^{\circ}t = 135^{\circ} - 5^{\circ}t$.
因为 $∠BOC = 2∠AOD$,
所以 $135^{\circ} - 5^{\circ}t = 2(5^{\circ}t - 120^{\circ})$,
所以 $t = 25$.
综上, $t$ 的值为21或25.
查看更多完整答案,请扫码查看


