《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

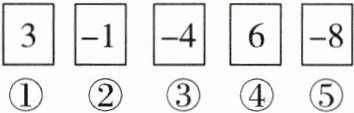
19. (14分)如图,小明有标注①~⑤号的5张写着不同有理数的卡片,请你按要求选出卡片,完成下列各题。
(1)从中选出1张卡片,且这张卡片的有理数在全部有理数大小排列里居中,应选取______号卡片；
(2)从中选出2张卡片,且这2张卡片的有理数的差最大,应选取______号卡片,差的最大值是______；
(3)从中选出3张卡片,且这3张卡片的有理数的积最小,应选取______号卡片,积的最小值是______；
(4)从中选出4张卡片,且将这4张卡片的有理数运用加、减、乘和除四则运算及括号列出一个算式,使得该算式的计算结果为24,请你写出算式(只需写出1种即可)。

答案：
(1)②
(2)④⑤ 14
(3)①④⑤ -144
(4)答案不唯一,如选取①②④⑤四张卡片.
$(-1-6÷3)×(-8)=(-1-2)×(-8)=(-3)×(-8)=24$.

20. (14分)观察下列解题过程。
计算：$1+5+5^{2}+5^{3}+... +5^{24}+5^{25}$。
解：设$S= 1+5+5^{2}+5^{3}+... +5^{24}+5^{25}$,①
则$5S= 5+5^{2}+5^{3}+... +5^{24}+5^{25}+5^{26}$,②
②-①,得$4S= 5^{26}-1$,$\therefore S= \frac{5^{26}-1}{4}$。
你能用上述方法计算下面这道题吗？
$1+3+3^{2}+3^{3}+... +3^{9}+3^{10}$。

答案： 设$S=1+3+3^{2}+3^{3}+... +3^{9}+3^{10}$, ①
则$3S=3+3^{2}+3^{3}+... +3^{10}+3^{11}$, ②
②-①,得$2S=3^{11}-1$,所以$S=\frac {3^{11}-1}{2}$.