《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

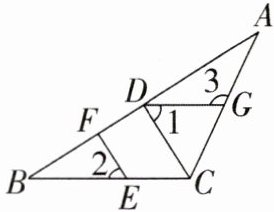
19. (8分)如图,在三角形$ABC$中,$CD⊥AB$,垂足为$D$,点$E在BC$上,$EF⊥AB$,垂足为$F$.
(1)$CD与EF$平行吗？为什么？
(2)如果$∠1= ∠2$,且$∠3= 115^{\circ }$,求$∠ACB$的度数.

答案：
(1) $ CD $ 与 $ EF $ 平行. 理由: 因为 $ CD \perp AB $, $ EF \perp AB $, 垂直于同一直线的两直线互相平行, 所以 $ CD // EF $.
(2) 由
(1)知 $ CD // EF $, 所以 $ \angle 2 = \angle BCD $.
又因为 $ \angle 1 = \angle 2 $, 所以 $ \angle 1 = \angle BCD $.
所以 $ DG // BC $. 所以 $ \angle ACB = \angle 3 = 115 ^ { \circ } $.

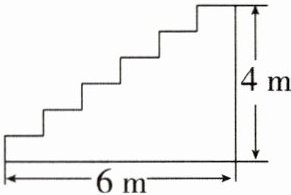
20. (8分)某宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽$2m$,其侧面如图所示,则买地毯至少需要多少元？

答案： 平移线段, 把楼梯的横、竖分别向上、向左平移, 构成一个矩形, 长、宽分别为 $ 6 \mathrm { ~m } $, $ 4 \mathrm { ~m } $, 所以地毯的长度为 $ 6 + 4 = 10 ( \mathrm { ~m } ) $, 地毯的面积为 $ 10 \times 2 = 20 ( \mathrm { ~m } ^ { 2 } ) $, 所以买地毯至少需要 $ 20 \times 40 = 800 $ (元).

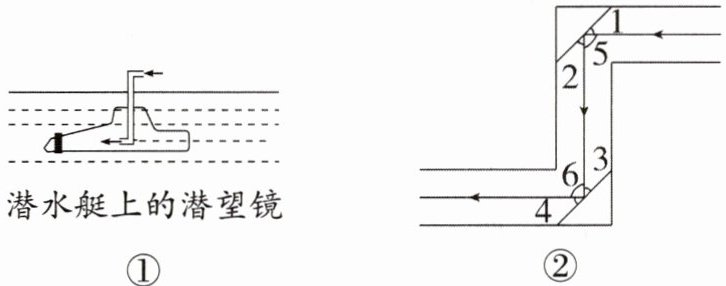
21. (10分)你知道潜水艇吗？它在军事上的作用非常大. 潜水艇下潜后,艇内人员可以用潜望镜来观察水面上的情况,如图①. 其实它的原理非常简单,如图②,潜望镜中的两个平面镜与水平方向的夹角都为$45^{\circ }$,光线经过镜子反射时,$∠1= ∠2$,$∠3= ∠4$. 你能解释为什么进入潜望镜的光线和离开潜望镜的光线是平行的吗？

答案： 因为 $ \angle 1 = \angle 2 = 45 ^ { \circ } $, $ \angle 3 = \angle 4 = 45 ^ { \circ } $, 所以 $ \angle 5 = 180 ^ { \circ } - 45 ^ { \circ } \times 2 = 90 ^ { \circ } $, $ \angle 6 = 180 ^ { \circ } - 45 ^ { \circ } \times 2 = 90 ^ { \circ } $, 所以 $ \angle 5 = \angle 6 $, 所以进入潜望镜的光线和离开潜望镜的光线是平行的.

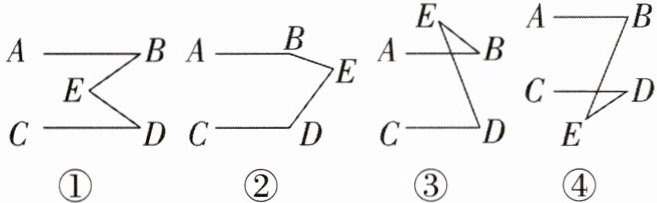
22. (10分)小明用《几何画板》画图,他先画了两条平行线$AB$,$CD$,然后在平行线间画了一点$E$,连结$BE$,$DE$(如图①)后,它用鼠标左键点住点$E$,拖动后,分别得到如图②、③、④的图形,这时他突然一想,$∠B$,$∠D与∠BED$之间的度数有没有某种联系呢？接着小明同学通过利用《几何画板》的“度量角度”和“计算”的功能,找到了这三个角之间的关系.
(1)请你分别写出图①至图④各图中的$∠B$,$∠D与∠BED$之间的关系；
(2)证明从图③中得到的结论.

答案：

(1) ① $ \angle B + \angle D = \angle BED $;
② $ \angle B + \angle D + \angle BED = 360 ^ { \circ } $;
③ $ \angle BED = \angle D - \angle B $;
④ $ \angle BED = \angle B - \angle D $.
(2) 如图, 过点E作 $ EF // AB $.
因为 $ AB // CD $,

所以 $ EF // CD $,
所以 $ \angle D = \angle DEF $, $ \angle B = \angle BEF $.
又因为 $ \angle BED = \angle DEF - \angle BEF $,
所以 $ \angle BED = \angle D - \angle B $.