第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
8. 在上午9时到10时之间,时钟的分针与时针会重合一次,这次的重合时间在()
A. 9:48~9:49之间
B. 9:49~9:50之间
C. 9:50~9:51之间
D. 9:51~9:52之间
A. 9:48~9:49之间
B. 9:49~9:50之间
C. 9:50~9:51之间
D. 9:51~9:52之间
答案:
B 解析:9时时,时针和分针呈 $270^{\circ}$,时针1分钟走 $0.5^{\circ}$,分针一分钟走 $6^{\circ}$.设9时 $x$ 分重合,则有 $0.5x + 270 = 6x$, $x = 49\frac{1}{11}$,故选B.
9. 三棱柱是由______个面围成的,五棱柱有______个顶点.
答案:
5 10
10. 如图,从小明家到学校有4条路,其中沿路线______走最近,其数学依据是______.
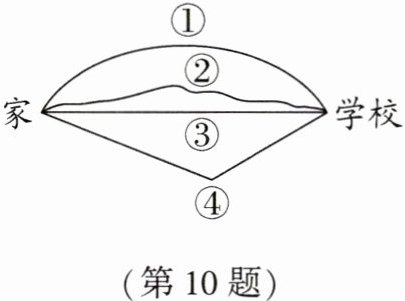

答案:
③ 两点之间线段最短
11. 计算:(1)54.26°= ______;
(2)78°18′-56°46′= ______.
(2)78°18′-56°46′= ______.
答案:
(1) $54^{\circ}15'36''$
(2) $21^{\circ}32'$
(1) $54^{\circ}15'36''$
(2) $21^{\circ}32'$
12. 如图,直线AB与CD相交于点O,∠1= ∠2,若∠AOE= 140°,则∠AOC的度数为______度.
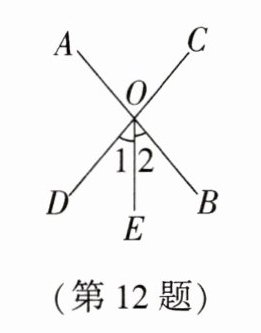

答案:
80
13. 如图,∠AOC和∠DOB都是直角,如果∠DOC= 28°,那么∠AOB= ______.
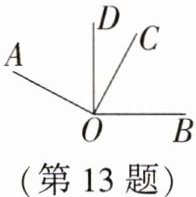

答案:
$152^{\circ}$
14. 如果线段AB= 10,点C,D在直线AB上,BC= 6,D是AC的中点,那么A,D两点间的距离是______.
答案:
2或8
15. 一列火车往返于A地与B地之间,途中有C,D,E三个车站停靠,那么往返于A,B两地之间的不同车票共有______种.
答案:
20
16. 如图,若∠3:∠2= 2:5,且∠2-∠1= 12°,则∠3等于______.
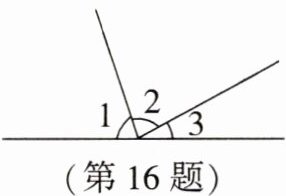

答案:
$32^{\circ}$ 解析:因为 $∠3:∠2 = 2:5$,
所以设 $∠3 = 2x$, $∠2 = 5x$.
因为 $∠1 + ∠2 + ∠3 = 180^{\circ}$, $∠2 - ∠1 = 12^{\circ}$,
所以 $5x - 12^{\circ} + 5x + 2x = 180^{\circ}$,解得 $x = 16^{\circ}$,
所以 $∠3 = 2×16^{\circ} = 32^{\circ}$.
所以设 $∠3 = 2x$, $∠2 = 5x$.
因为 $∠1 + ∠2 + ∠3 = 180^{\circ}$, $∠2 - ∠1 = 12^{\circ}$,
所以 $5x - 12^{\circ} + 5x + 2x = 180^{\circ}$,解得 $x = 16^{\circ}$,
所以 $∠3 = 2×16^{\circ} = 32^{\circ}$.
17. (8分)动手操作.如图,平面内有A,B,C,D四点,按下列语句画图:
(1)画射线AB,直线BC,线段AC;
(2)延长线段CA;
(3)连结AD并反向延长与BC相交于点E.
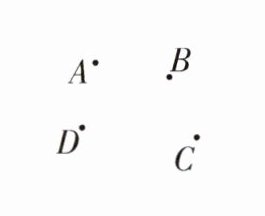
(1)画射线AB,直线BC,线段AC;
(2)延长线段CA;
(3)连结AD并反向延长与BC相交于点E.
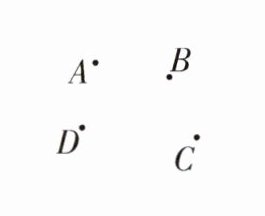
答案:
(1)如图所示:

(2)如图所示:

(3)如图所示:

(1)如图所示:

(2)如图所示:

(3)如图所示:

18. (8分)如图,已知线段a,b,c(a>c),用圆规和直尺画一条线段,使它等于a+2b-c.
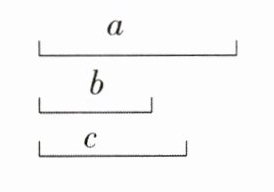
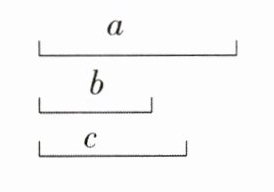
答案:
线段$AE$就是所求作的线段,$AE=a + 2b - c$。
19. (8分)如图,C是线段AB上一点,AC<CB,M,N分别是AB,CB的中点,AC= 8,NB= 5,求线段MN的长.


答案:
因为 $N$ 是 $CB$ 的中点, $NB = 5$,所以 $BC = 10$.因为 $AC = 8$,所以 $AB = AC + CB = 18$.因为 $M$ 是 $AB$ 的中点,所以 $MB = \frac{1}{2}AB = 9$,所以 $MN = MB - NB = 9 - 5 = 4$.
查看更多完整答案,请扫码查看


