《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

16. 如图,正方形$ABCD$内部有若干个点,用这些点以及正方形$ABCD的顶点A,B,C,D$把原正方形分割成一些三角形(互相不重叠).

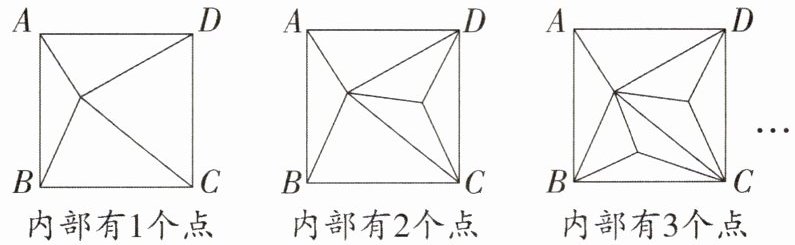
(1)填写下表：

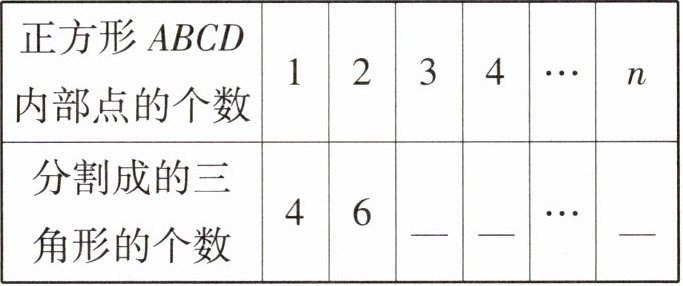
(2)原正方形能否被分割成4052个三角形？若能,则此时正方形$ABCD$内部有多少个点？若不能,请说明理由.

答案：
(1)8 10 $2(n+1)$
(2)能.设点数为n，则$2(n+1)=4052$，解得$n=2025$.即原正方形能被分割成4052个三角形，此时正方形ABCD内部有2025个点.

17. 观察下列等式：
12×231 = 132×21；
13×341 = 143×31；
23×352 = 253×32；
34×473 = 374×43；
62×286 = 682×26；
…以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.(1)根据上述各式反映的规律填空,使式子成为“数字对称等式”：①52×______=______×25；②______×396 = 693×______.(2)设这类等式左边两位数的十位上的数字为a,个位上的数字为b,且$2\leq a + b\leq9,$写出表示“数字对称等式”一般规律的式子(含a,b),并说明理由.

答案：
(1)①275 572 ②63 36
(2)因为左边两位数的十位上的数字为a，个位上的数字为b，所以左边的两位数是$10a+b$，三位数是$100b+10(a+b)+a$，右边的两位数是$10b+a$，三位数是$100a+10(a+b)+b$，一般规律为$(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a)$.
　理由:因为左边$=(10a+b)×[100b+10(a+b)+a]$
　　$=(10a+b)×(100b+10a+10b+a)$
　$=(10a+b)×(110b+11a)$
　$=11(10a+b)×(10b+a)$，
　右边$=[100a+10(a+b)+b]×(10b+a)$
　$=(100a+10a+10b+b)×(10b+a)$
　$=(110a+11b)×(10b+a)$
　$=11(10a+b)×(10b+a)$，
　所以左边=右边.