第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 下列各数中,与$-\frac {1}{2}$互为相反数的是()
A. 2
B. -2
C. $\frac {1}{2}$
D. $-\frac {1}{2}$
A. 2
B. -2
C. $\frac {1}{2}$
D. $-\frac {1}{2}$
答案:
C
2. 某冰箱冷藏室的温度是$5^{\circ }C$,冷冻室的温度比冷藏室的温度低$17^{\circ }C$,则冷冻室的温度是()
A. $12^{\circ }C$
B. $-12^{\circ }C$
C. $22^{\circ }C$
D. $-22^{\circ }C$
A. $12^{\circ }C$
B. $-12^{\circ }C$
C. $22^{\circ }C$
D. $-22^{\circ }C$
答案:
B
3. 同种液体,压强随着深度增加而增大.7 km深处海水的压强为72 100 000 Pa,数据72 100 000用科学记数法表示为()
A. $7.21×10^{6}$
B. $0.721×10^{8}$
C. $7.21×10^{7}$
D. $721×10^{5}$
A. $7.21×10^{6}$
B. $0.721×10^{8}$
C. $7.21×10^{7}$
D. $721×10^{5}$
答案:
C
4. 下列各式计算正确的是()
A. $4m^{2}n-2mn^{2}= 2mn$
B. $-2a+5b= 3ab$
C. $4xy-3xy= xy$
D. $a^{2}+a^{2}= a^{4}$
A. $4m^{2}n-2mn^{2}= 2mn$
B. $-2a+5b= 3ab$
C. $4xy-3xy= xy$
D. $a^{2}+a^{2}= a^{4}$
答案:
C
5. 一副三角尺按如图所示的方式摆放,且$∠1比∠2大50^{\circ }$,则$∠2$的度数为()
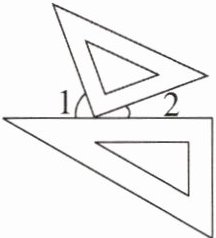
A. $20^{\circ }$
B. $50^{\circ }$
C. $70^{\circ }$
D. $30^{\circ }$

A. $20^{\circ }$
B. $50^{\circ }$
C. $70^{\circ }$
D. $30^{\circ }$
答案:
A
6. 如图,在数轴上表示实数$\sqrt {14}$的点可能是()
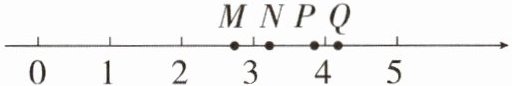
A. 点M
B. 点N
C. 点P
D. 点Q
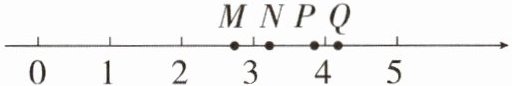
A. 点M
B. 点N
C. 点P
D. 点Q
答案:
C
7. 各个数位上数的立方和等于其本身的三位数叫作“水仙花数”.比如153是“水仙花数”,因为$1^{3}+5^{3}+3^{3}= 153$.以下四个数中是“水仙花数”的是()
A. 113
B. 220
C. 345
D. 407
A. 113
B. 220
C. 345
D. 407
答案:
D
8. 在一次美化校园活动中,先安排34人去拔草,18人去植树,后又增派20人去支援他们,结果拔草的人数是植树人数的2倍,问支援拔草和支援植树的分别有多少人?若设支援拔草的有x人,则下列方程中正确的是()
A. $34+x= 2×18$
B. $34+x= 2(38-x)$
C. $34-x= 2(18+x)$
D. $34-x= 2×18$
A. $34+x= 2×18$
B. $34+x= 2(38-x)$
C. $34-x= 2(18+x)$
D. $34-x= 2×18$
答案:
B 解析:设支援拔草的有x人,则支援植树的有(20 - x)人,现在拔草的总人数为(34 + x)人,植树的总人数为18 + 20 - x = (38 - x)人.根据等量关系列方程得,34 + x = 2(38 - x).故选 B.
9. 如图所示,OB,OC是$∠AOD$内的任意两条射线,OM平分$∠AOB$,ON平分$∠COD$,若$∠MON= α,∠BOC= β$,则表示$∠AOD$的代数式是()
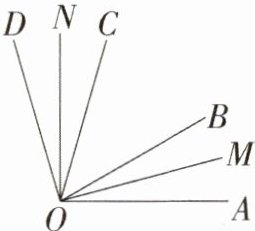
A. $2α-β$
B. $α-β$
C. $α+β$
D. 以上都不正确

A. $2α-β$
B. $α-β$
C. $α+β$
D. 以上都不正确
答案:
A 解析:因为∠MON = α,∠BOC = β,
所以∠MON - ∠BOC = ∠CON + ∠BOM = α - β.
又因为OM平分∠AOB,ON平分∠COD,
所以∠CON = ∠DON,∠AOM = ∠BOM;
由题意得∠AOD = ∠MON + ∠DON + ∠AOM = ∠MON + ∠CON + ∠BOM = α+(α - β)=2α - β.
所以∠MON - ∠BOC = ∠CON + ∠BOM = α - β.
又因为OM平分∠AOB,ON平分∠COD,
所以∠CON = ∠DON,∠AOM = ∠BOM;
由题意得∠AOD = ∠MON + ∠DON + ∠AOM = ∠MON + ∠CON + ∠BOM = α+(α - β)=2α - β.
查看更多完整答案,请扫码查看


