《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

10. 我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10,…)和“正方形数”(如1,4,9,16,…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则$m+n$的值为()

A. 33
B. 301
C. 386
D. 571

答案： C

11. $-\frac {1}{4}$的倒数是____,-8的立方根是____,$\sqrt {16}= $____.

答案： -4 -2 4

12. 若$-\frac {1}{2}x^{m+3}y与2x^{4}y^{n+3}$是同类项,则$(m+n)^{8888}= $____.

答案： 1

13. 如果多项式$-2a+3b+8$的值为5,那么多项式$9b-6a+2$的值等于____.

答案： -7

14. 如图,线段$AB= 8cm$,点C为线段AB上一点,$BC= 2cm$,点D,E分别为AC和AB的中点,则线段DE的长为____cm.

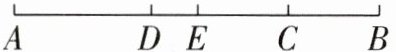
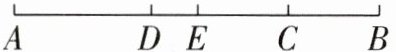
答案： 1 解析:因为AB = 8 cm,BC = 2 cm,所以AC = AB - BC = 8 - 2 = 6(cm).因为点D,E分别为AC和AB的中点，所以AD = $\frac{1}{2}$AC = $\frac{1}{2}$×6 = 3(cm),AE = $\frac{1}{2}$AB = $\frac{1}{2}$×8 = 4(cm),所以DE = AE - AD = 4 - 3 = 1(cm).

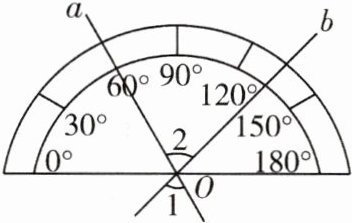
15. 如图,直线a,b相交于点O,将量角器的中心与点O重合,发现表示$60^{\circ }$的点在直线a上,表示$135^{\circ }$的点在直线b上,则

$∠1= $____$^{\circ }$.

答案： 75 解析:因为∠2 = 135° - 60° = 75°,所以∠1 = ∠2 = 75°,故答案为75.

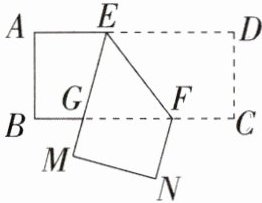
16. 如图所示,把一张长方形纸片ABCD沿EF折叠,若$∠EFB= 58^{\circ }$,则$∠BFN= $____.

答案： 64° 解析:因为四边形MNFE由四边形CDEF折叠而成,∠EFB = 58°,所以∠EFC = ∠EFN = 180° - 58° = 122°,所以∠BFN = ∠EFN - ∠EFB = 122° - 58° = 64°.

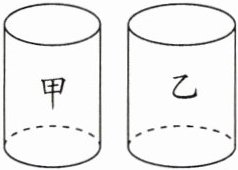
17. 如图,在水平桌面上有甲、乙两个圆柱形的容器,内部底面积分别为$80cm^{2}$、$100cm^{2}$,且甲容器装满水,乙容器是空的.若将甲容器中的水全部倒入乙容器中,则乙容器中的水位高度比原先甲容器中的水位高度低了8 cm,则甲容器的高度是____.

答案： 40 cm

18. 如图,数轴上O为原点,A点对应的数为x,一动点P从点A出发,按以下规律跳动：第1次跳动到AO的中点$A_{1}$处,第2次从$A_{1}点跳动到A_{1}O的中点A_{2}$处,第3次从$A_{2}点跳动到A_{2}O的中点A_{3}$处.按照这样的规律跳动到点$A_{4},A_{5},A_{6},...,A_{n}$(n是整数)处,若$A_{2}表示的数为(\frac {1}{2}-\frac {1}{4}x)$,则点$A_{2025}$在数轴上对应的数为____.

答案： $\frac{1}{2^{2025}}$ 解析:因为A₁是AO的中点,A₂是A₁O的中点，所以$\frac{1}{2}$ - $\frac{1}{4}$x = $\frac{1}{4}$x,解得x = 1.所以数轴上O,A两点的距离为1,即OA = 1.因为动点P从点A出发,第1次跳动到AO的中点A₁处，所以点A₁与点O的距离为$\frac{1}{2}$.同理可得，点A₂与点O的距离为$\frac{1}{2^{2}}$，点A₃与点O的距离为$\frac{1}{2^{3}}$……以此类推，点Aₙ与点O的距离为$\frac{1}{2^{n}}$.当n = 2025时，点A₂₀₂₅与点O的距离为$\frac{1}{2^{2025}}$.

19. (8分)计算：
(1)$-(-6)×(-\frac {1}{3})-2$；
(2)$-1^{4}÷(-5)^{2}×(-\frac {5}{3})+|0.8-1|$.

答案：
(1) -4
(2) $\frac{4}{15}$