《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

20. (8分)先化简,再求值：$-5a^{2}-[2a-(3a-4a^{2})+a^{2}]$,其中$a= -1$.

答案： 原式 = -5a² - 2a + 3a - 4a² - a² = -10a² + a,当a = -1时,原式 = -10 - 1 = -11.

21. (10分)解下列方程：
(1)$3-(5-2x)= x+2$；
(2)$\frac {2-x}{4}-1= \frac {3-2x}{3}$.

答案：
(1)去括号,得3 - 5 + 2x = x + 2,
移项、合并同类项,得x = 4.
(2)去分母,得6 - 3x - 12 = 12 - 8x,
移项、合并同类项,得5x = 18,
解得x = 3.6.

22. (12分)已知多项式$-2x^{2}y^{3}-4$中,含字母项的系数记为a,多项式的次数记为b,常数项记为c,且a,b,c分别是点A,点B,点C在数轴上对应的数.
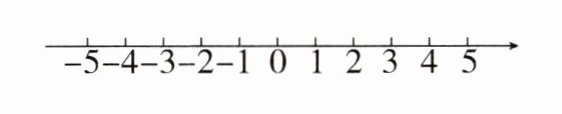
(1)求出a,b,c的值,并在如图所示的数轴上表示出点A,点B和点C.
(2)若A,B,C三点同时出发,沿数轴的负方向运动,它们的速度分别为2个单位长度/秒,3个单位长度/秒,$\frac {3}{4}$个单位长度/秒,请问经过多少秒,B追上了C？此时A是否也追上了C？(要求具体说明)

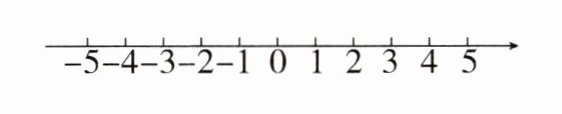
答案：
(1)a = -2,b = 2 + 3 = 5,c = -4.如图所示.
-5 -4 -3 -2 -1 0 1 2 3 4 5
(2)设经过x秒B追上了C,由题意,得
3x = 9 + $\frac{3}{4}$x,解得x = 4,故经过4秒B追上了C.
(2 - $\frac{3}{4}$)×4 = 5 ＞ 2,
所以此时A已经追上了C.