《2025年暑假总动员宁夏人民教育出版社七升八数学浙教版》

9. 若$\begin{cases}x = a,\\y = b\end{cases}是方程3x + y = 1$的解,则$9a + 3b + 1 = $______.

答案： 4

10. 已知关于$x的一元一次方程\frac{x}{2025} + 8 = 2025x + a的解为x = -6$,那么关于$y的一元一次方程\frac{6 - y}{2025} + 8 = 2025(6 - y) + a的解为y = $______.

答案： 12

11. 在图中月历上,任意圈出一个由$3$个相邻的数组成的竖列,如果它们的和为$48$,那么其中日期最小的一天是该月______号.

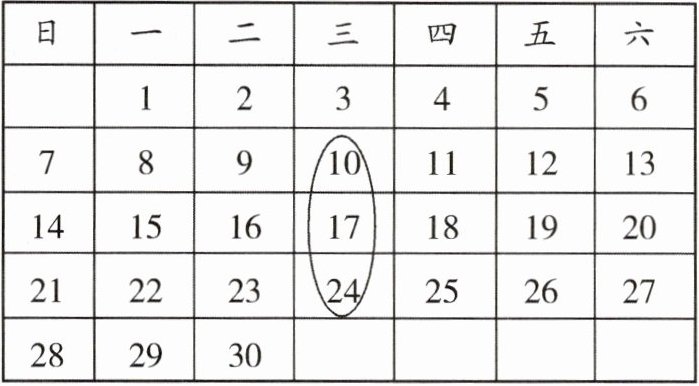
答案： 9

12. 《一千零一夜》中有这样一段文字：有一群鸽子,其中一部分在树上欢歌,另一部分在地上觅食,树上一只鸽子对地上觅食的鸽子说：“若从你们中飞来一只,则树下的鸽子就是整个鸽群的$\frac{1}{3}$；若从树上飞下去一只,则树上、树下的鸽子数一样多.”树上有______只鸽子,树下有______只鸽子.

答案： 7 5

13. 关于$x的方程\frac{3 - 2x}{x - 3} + \frac{2 + mx}{3 - x} = -1$无解,则$m = $______.

答案： -1 或 $-\frac{5}{3}$

14. 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它本身的$\frac{1}{3}$,另一根露出水面的长度是它本身的$\frac{1}{5}$.两根铁棒长度之和为$55cm$,此时木桶中水的深度是______$cm$.

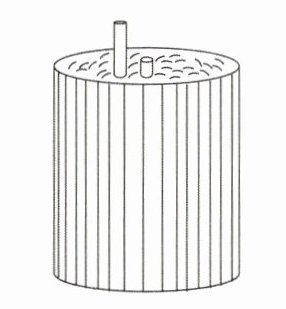
答案： 20

15. 小亮在匀速行驶的汽车里,注意到公路里程碑上的数如下：

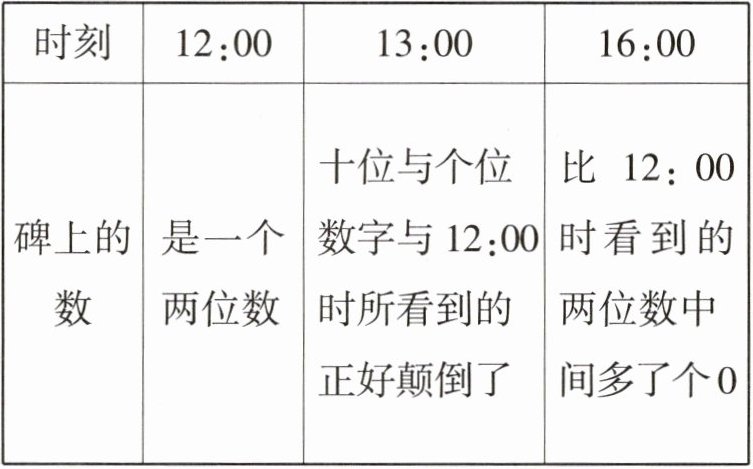
则12:00时小亮看到的两位数是______.

答案： 27 解析:设小亮 12:00 时看到的两位数的个位数为x,十位数为 y,汽车行驶速度为 v,根据题意得
$\left\{ \begin{array} { l } { 1 0 x + y - ( 1 0 y + x ) = v , } \\ { 1 0 0 y + x - ( 1 0 y + x ) = 4 v , } \end{array} \right.$
解得 $x = \frac { 7 } { 2 } y$.
因为 x,y 为 1~9 内的自然数,
所以 $x = 7 , y = 2$,
所以小亮 12:00 时看到的两位数是 27.

16. 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密).已知加密规则为：明文$a$,$b$,$c$,$d对应的密文为a + b$,$b + c$,$c + d$,$d + 2a$.例如：明文1,2,3,4对应的密文为3,5,7,6.当接收方收到密文8,11,15,15时,则解密得到的明文应为______.

答案： 3,5,6,9 解析:设密文 8,11,15,15 分别对应的明文为 a,b,c,d,由题意得
$\left\{ \begin{array} { l } { a + b = 8 , } \\ { b + c = 1 1 , } \\ { c + d = 1 5 , } \\ { d + 2 a = 1 5 , } \end{array} \right.$
解得
$\left\{ \begin{array} { l } { a = 3 , } \\ { b = 5 , } \\ { c = 6 , } \\ { d = 9 . } \end{array} \right.$