《2025年课时夺冠九年级数学上册湘教版》

1. 在$Rt△ABC$中,$∠C= 90^{\circ }$,$BC= 3$,$AC= 4$,则$tanA$的值为()
A. $\frac {3}{4}$
B. $\frac {4}{3}$
C. $\frac {3}{5}$
D. $\frac {4}{5}$

答案： A

2. 如图,在$Rt△ABC$中,$∠C= 90^{\circ }$,$AC= 4$,$tanA= \frac {1}{2}$,则$BC$的长是()

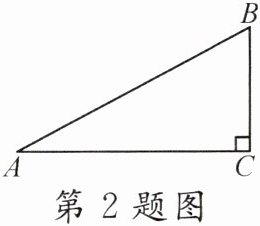
A. 2
B. 8
C. $2\sqrt {5}$
D. $4\sqrt {5}$

答案： A

3. (永州零陵区期末)如图,$△ABC$的顶点都在正方形网格的格点上,则$tan∠BAC$的值是()

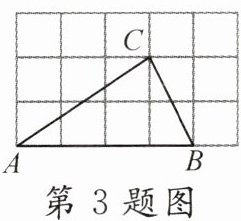
A. $\frac {1}{2}$
B. 2
C. $\frac {2}{3}$
D. $\frac {3}{2}$

答案： C

4. 如图,在$△ABC$中,$∠C= 90^{\circ }$,$BC= 3$,$AB= 6$,求$tanA$,$tanB$的值.

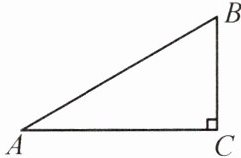
答案： 解：在 $ Rt\triangle ABC $ 中，$ AC = \sqrt{AB^{2} - BC^{2}} = \sqrt{6^{2} - 3^{2}} = 3\sqrt{3} $，$ \therefore \tan A = \frac{BC}{AC} = \frac{3}{3\sqrt{3}} = \frac{\sqrt{3}}{3} $，$ \tan B = \frac{AC}{BC} = \frac{3\sqrt{3}}{3} = \sqrt{3} $。

5. (邵阳绥宁县一模)$3tan30^{\circ }$的值为()
A. 1
B. $\sqrt {2}$
C. $\sqrt {3}$
D. 2

答案： C

6. 在$△ABC$中,$∠C= 90^{\circ }$,$tanA= \sqrt {3}$,则$∠B$的度数为()
A. $30^{\circ }$
B. $45^{\circ }$
C. $60^{\circ }$
D. $90^{\circ }$

答案： A

7. 计算：
(1)$tan60^{\circ }+tan45^{\circ }-3tan30^{\circ }$；
(2)$2tan30^{\circ }-tan45^{\circ }-\sqrt {(1-tan60^{\circ })^{2}}$.

答案： 解：
(1) 原式 $ = \sqrt{3} + 1 - 3 \times \frac{\sqrt{3}}{3} = 1 $。
(2) 原式 $ = 2 \times \frac{\sqrt{3}}{3} - 1 - (\sqrt{3} - 1) = -\frac{\sqrt{3}}{3} $。

8. 用计算器计算$tan17^{\circ }42'$的结果约是(结果精确到0.0001)()
A. 0.3189
B. 0.3190
C. 0.3191
D. 0.3192

答案： C

9. 填空(结果精确到$0.1^{\circ }$)：
(1)已知$tanα= 0.2717$,则$α\approx $____；
(2)已知$tanα= 1.5108$,则$α\approx $____.

答案：
(1) $ 15.2^{\circ} $
(2) $ 56.5^{\circ} $

10. (衡阳耒阳市期末)在$Rt△ABC$中,$∠C= 90^{\circ }$,$AC= 12$,$BC= 5$,则下列各式中正确的是()
A. $tanA= \frac {5}{12}$
B. $tanA= \frac {5}{13}$
C. $sinA= \frac {5}{12}$
D. $cosA= \frac {5}{12}$

答案： A

11. 如图,在$△ABC$中,$∠C= 90^{\circ }$,$AC= 24$,$BC= 7$,求$sinA$,$cosA$,$tanA$的值.

答案： 解：在 $ Rt\triangle ABC $ 中，$ AB = \sqrt{AC^{2} + BC^{2}} = 25 $，$ \therefore \sin A = \frac{BC}{AB} = \frac{7}{25} $，$ \cos A = \frac{AC}{AB} = \frac{24}{25} $，$ \tan A = \frac{BC}{AC} = \frac{7}{24} $。