第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 某公司现有原材料 100t,每天平均用去 x t.若这批原材料能用 y 天,则 y 与 x 之间的函数表达式为()
A. $ y = 100x $
B. $ y = \frac { 100 } { x } $
C. $ y = \frac { x } { 2 } + 100 $
D. $ y = 100 - x $
A. $ y = 100x $
B. $ y = \frac { 100 } { x } $
C. $ y = \frac { x } { 2 } + 100 $
D. $ y = 100 - x $
答案:
B
2. 一台印刷机每年可印刷的书本数量 y(万册)与它的使用时间 x(年)成反比例关系,且当 $ x = 2 $时,$ y = 20 $,则 y 与 x 的函数图象大致是()
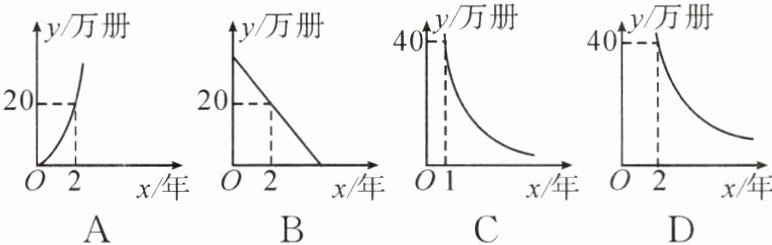

答案:
C
3. (张家界永定区期末)一定体积的面团做成拉面时,面条的总长度 y(m)是面条的粗细(横截面积)$ S ( mm ^ { 2 } ) $的反比例函数,其图象如图所示.
(1)写出 y 与 S 之间的函数表达式;
(2)当面条的横截面积为 $ 2 mm ^ { 2 } $时,面条的总长度是多少米?
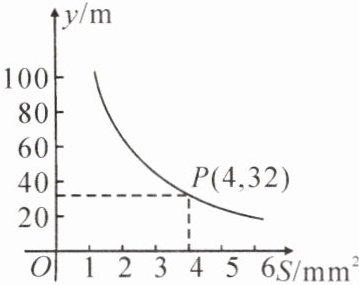
(1)写出 y 与 S 之间的函数表达式;
(2)当面条的横截面积为 $ 2 mm ^ { 2 } $时,面条的总长度是多少米?

答案:
解:
(1)设 $ y $ 与 $ S $ 之间的函数表达式为 $ y = \frac{k}{S} $。将点 $ (4, 32) $ 代入,得 $ k = 4 \times 32 = 128 $,$\therefore y $ 与 $ S $ 之间的函数表达式为 $ y = \frac{128}{S}(S > 0) $。
(2)当 $ S = 2 $ 时,$ y = \frac{128}{2} = 64 $。答:当面条横截面积为 $ 2 \mathrm{mm}^2 $ 时,面条的总长度是 $ 64 \mathrm{m} $。
(1)设 $ y $ 与 $ S $ 之间的函数表达式为 $ y = \frac{k}{S} $。将点 $ (4, 32) $ 代入,得 $ k = 4 \times 32 = 128 $,$\therefore y $ 与 $ S $ 之间的函数表达式为 $ y = \frac{128}{S}(S > 0) $。
(2)当 $ S = 2 $ 时,$ y = \frac{128}{2} = 64 $。答:当面条横截面积为 $ 2 \mathrm{mm}^2 $ 时,面条的总长度是 $ 64 \mathrm{m} $。
4. (怀化中考)已知压力 $ F ( N ) $、压强 $ P ( Pa ) $与受力面积 $ S ( m ^ { 2 } ) $之间满足关系式 $ F = P S $.当 F 为定值时,图中大致表示压强 P 与受力面积 S 之间的函数关系的是()
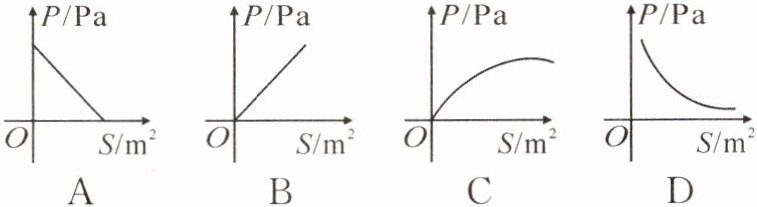

答案:
D
5. 一定质量的氧气,它的密度 $ \rho ( kg / m ^ { 3 } ) $是它的体积 $ V ( m ^ { 3 } ) $的反比例函数.当 $ V = 20 m ^ { 3 } $时,$ \rho = 1.36 kg / m ^ { 3 } $;当 $ V = 40 m ^ { 3 } $时,$ \rho = $______ $ kg / m ^ { 3 } $.
答案:
$ 0.68 $
6. (邵阳武冈市期中)某气球内充满了一定量的气体,当温度不变时,气球内气体的气压 $ p ( kPa ) $是气体体积 $ V ( m ^ { 3 } ) $的反比例函数,其图象如图所示.
(1)求这个函数的表达式;
(2)当气体体积为 $ 1 m ^ { 3 } $时,气压是多少?
(3)当气球内的气压大于 140 kPa 时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(结果精确到 $ 0.01 m ^ { 3 } $)
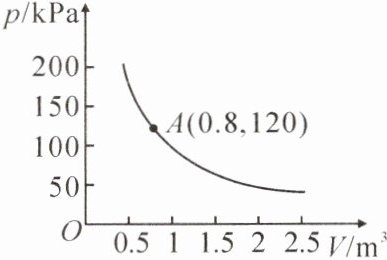
(1)求这个函数的表达式;
(2)当气体体积为 $ 1 m ^ { 3 } $时,气压是多少?
(3)当气球内的气压大于 140 kPa 时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(结果精确到 $ 0.01 m ^ { 3 } $)

答案:
解:
(1)设这个函数的表达式是 $ p = \frac{k}{V} $。将点 $ (0.8, 120) $ 代入,得 $ 120 = \frac{k}{0.8} $,解得 $ k = 96 $,$\therefore $ 这个函数的表达式是 $ p = \frac{96}{V} $。
(2)当 $ V = 1 $ 时,$ p = \frac{96}{1} = 96 $,$\therefore $ 当气体体积为 $ 1 \mathrm{m}^3 $ 时,气压是 $ 96 \mathrm{kPa} $。
(3)当 $ p = 140 $ 时,$ V = \frac{96}{140} \approx 0.69 $,$\therefore $ 为了安全起见,气体的体积应不小于 $ 0.69 \mathrm{m}^3 $。
(1)设这个函数的表达式是 $ p = \frac{k}{V} $。将点 $ (0.8, 120) $ 代入,得 $ 120 = \frac{k}{0.8} $,解得 $ k = 96 $,$\therefore $ 这个函数的表达式是 $ p = \frac{96}{V} $。
(2)当 $ V = 1 $ 时,$ p = \frac{96}{1} = 96 $,$\therefore $ 当气体体积为 $ 1 \mathrm{m}^3 $ 时,气压是 $ 96 \mathrm{kPa} $。
(3)当 $ p = 140 $ 时,$ V = \frac{96}{140} \approx 0.69 $,$\therefore $ 为了安全起见,气体的体积应不小于 $ 0.69 \mathrm{m}^3 $。
查看更多完整答案,请扫码查看


