《2025年课时夺冠九年级数学上册湘教版》

10. 已知两个相似三角形的面积之比为$4 : 9$,这两个三角形的周长的和为100 cm,那么较小的三角形的周长为()
A. 20 cm
B. 30 cm
C. 40 cm
D. 60 cm

答案： C

11. (永州东安县期末)如图,将$\triangle ABC$沿边BC上的中线AD平移到$\triangle A ^ { \prime } B ^ { \prime } C ^ { \prime }$的位置. 已知$\triangle ABC$的面积为16,阴影部分三角形的面积为9. 若$A A ^ { \prime } = 1$,则$A ^ { \prime } D$的长为()

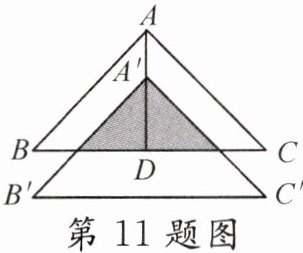
A. 2
B. 3
C. 4
D. $\frac { 3 } { 2 }$

答案： B

12. 如图,$\triangle ABC是面积为18 \mathrm { cm } ^ { 2 }$的等边三角形,被一平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积为______$\mathrm { cm } ^ { 2 }$.

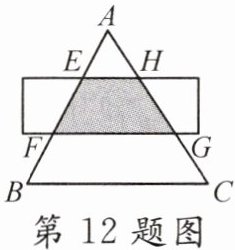
答案： 6

13. 如图,在$\square A B C D$中,E是CD的延长线上一点,BE与AD相交于点F,$D E = \frac { 1 } { 2 } C D$. 若$\triangle D E F$的面积为2,求$\square A B C D$的面积.

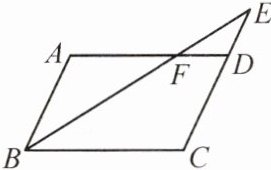
答案： 解：$\because$ 四边形$ABCD$是平行四边形，$\therefore AD// BC,AB// CD,AB = CD,\therefore \triangle DEF\backsim \triangle CEB,\triangle DEF\backsim$
$\triangle ABF.\because DE = \frac{1}{2}CD,\therefore DE = \frac{1}{3}CE,DE = \frac{1}{2}AB,\therefore \frac{S_{\triangle DEF}}{S_{\triangle CEB}} = (\frac{DE}{CE})^2 = \frac{1}{9}$，
$\frac{S_{\triangle DEF}}{S_{\triangle ABF}} = (\frac{DE}{AB})^2 = \frac{1}{4}.\because S_{\triangle DEF} = 2,\therefore S_{\triangle CEB} = 18,S_{\triangle ABF} = 8,\therefore S_{四边形BCDF} = S_{\triangle CEB} -$
$S_{\triangle DEF} = 16,\therefore S_{\square ABCD} = S_{四边形BCDF} + S_{\triangle ABF} = 16 + 8 = 24$.

14. 如图,在平面直角坐标系中,$Rt \triangle ABO$的顶点O与原点重合,顶点B在x轴的负半轴上,$\angle A B O = 90 ^ { \circ }$,OA与反比例函数$y = \frac { k } { x } ( x ＜ 0 )$的图象交于点D,且$O D = 2 A D$,过点D作x轴的垂线交x轴于点C. 若$S _ { 四边形 A B C D } = 10$,求k的值.

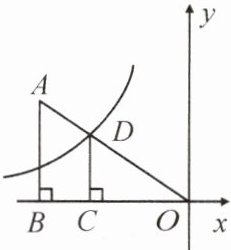
答案： 解：$\because OD = 2AD$，
$\therefore \frac{OD}{OA} = \frac{2}{3}.\because DC\perp OB,AB\perp OB,\therefore CD// AB,\therefore \triangle OCD\backsim \triangle OBA$，
$\therefore \frac{S_{\triangle OCD}}{S_{\triangle OBA}} = (\frac{OD}{OA})^2 = \frac{4}{9},\therefore \frac{S_{\triangle OCD}}{S_{四边形ABCD}} = \frac{4}{5}.\because S_{四边形ABCD} = 10,\therefore S_{\triangle OCD} = 8$.
$\because$ 点$D$在$y = \frac{k}{x}$的图象上，$\therefore |k| = 2S_{\triangle OCD} = 16$. 由图象知$k ＜ 0$，$\therefore k = -16$.

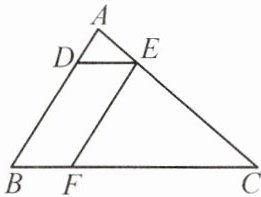
15. (怀化通道县期末)如图,在$\triangle ABC$中,点D,E,F分别在边AB,AC,BC上,连接DE,EF. 已知四边形BFED是平行四边形,$\frac { D E } { B C } = \frac { 1 } { 4 }$.
(1)若$A B = 8$,求线段AD的长；
(2)若$\triangle A D E$的面积为1,求平行四边形BFED的面积.

答案： 解：（1）$\because$ 四边形$BFED$是平行四边形，$\therefore DE// BF$，即$DE// BC$，
$\therefore \triangle ADE\backsim \triangle ABC,\therefore \frac{AD}{AB} = \frac{DE}{BC} = \frac{1}{4}.\because AB = 8,\therefore AD = 2$. （2）由（1）知
$\triangle ADE\backsim \triangle ABC,\therefore \frac{S_{\triangle ADE}}{S_{\triangle ABC}} = (\frac{DE}{BC})^2 = (\frac{1}{4})^2 = \frac{1}{16}.\because S_{\triangle ADE} = 1,\therefore S_{\triangle ABC} = 16$.
$\because$ 四边形$BFED$是平行四边形，$\therefore EF// AB,EF = BD,\therefore \triangle EFC\backsim \triangle ABC$. 由
（1）知$\frac{AD}{AB} = \frac{1}{4},\therefore \frac{BD}{AB} = \frac{3}{4},\therefore \frac{EF}{AB} = \frac{3}{4},\therefore \frac{S_{\triangle EFC}}{S_{\triangle ABC}} = (\frac{EF}{AB})^2 = (\frac{3}{4})^2 = \frac{9}{16}$，
$\therefore S_{\triangle EFC} = 9,\therefore S_{\square BFED} = S_{\triangle ABC} - S_{\triangle EFC} - S_{\triangle ADE} = 6$.