《2025年课时夺冠九年级数学上册湘教版》

11. 若一次函数 $ y = - x - 1 $ 的图象与反比例函数 $ y = \frac { k } { x } $ 的图象交于点 $ A ( 1 , a ) $ ,则k的值为()
A. 1
B. 2
C. -1
D. -2

答案： D

12. (永州道县模拟)若 $ a b ＜ 0 $ ,则一次函数 $ y = a x + b $ 与反比例函数 $ y = \frac { b } { x } $ 在同一平面直角坐标系中的图象大致可能是()

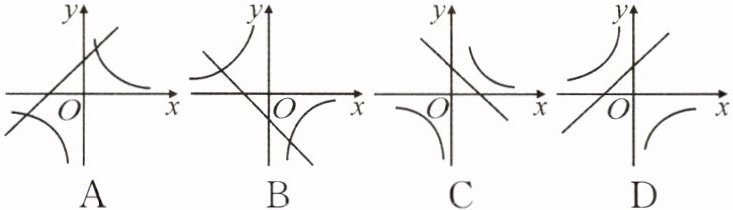
A.
B.
C.
D.

答案： C

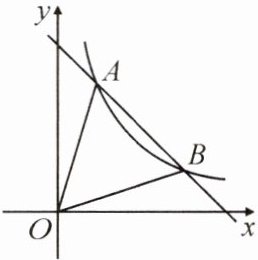
13. (长沙开福区期末)如图,双曲线 $ y _ { 1 } = \frac { k _ { 1 } } { x } ( x ＞ 0 ) $ 与直线 $ y _ { 2 } = k _ { 2 } x + b $ 交于 $ A ( 1,3 ) , B ( m , 1 ) $ 两点.
(1)求双曲线 $ y _ { 1 } = \frac { k _ { 1 } } { x } ( x ＞ 0 ) $ 与直线 $ y _ { 2 } = k _ { 2 } x + b $ 的表达式;
(2)根据第一象限图象观察,当 $ y _ { 1 } ＜ y _ { 2 } $ 时,x的取值范围是____;
(3)求 $ \triangle A O B $ 的面积.

答案： 解：
(1) 把点 $ A ( 1 , 3 ) $ 代入 $ y _ { 1 } = \frac { k _ { 1 } } { x } ( x ＞ 0 ) $，得 $ 3 = \frac { k _ { 1 } } { 1 } $，解得 $ k _ { 1 } = 3 $，
∴ 双曲线的表达式为 $ y _ { 1 } = \frac { 3 } { x } ( x ＞ 0 ) $。把点 $ B ( m , 1 ) $ 代入 $ y _ { 1 } = \frac { 3 } { x } ( x ＞ 0 ) $，得 $ 1 = \frac { 3 } { m } $，解得 $ m = 3 $，
∴ $ B ( 3 , 1 ) $。把点 $ A ( 1 , 3 ) $，$ B ( 3 , 1 ) $ 代入 $ y _ { 2 } = k _ { 2 } x + b $，得 $ \left\{ \begin{array} { l } { 3 = k _ { 2 } + b , } \\ { 1 = 3 k _ { 2 } + b , } \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { k _ { 2 } = - 1 , } \\ { b = 4 , } \end{array} \right. $
∴ 直线的表达式为 $ y _ { 2 } = - x + 4 $。
(2) $ 1 ＜ x ＜ 3 $
(3) 过点 A 作 $ A M \perp y $ 轴于点 M，过点 B 作 $ B N \perp x $ 轴于点 N，反向延长 AM，BN 相交于点 C。$ \because A ( 1 , 3 ) $，$ B ( 3 , 1 ) $，$ \therefore C ( 3 , 3 ) $，$ \therefore S _ { \triangle A O B } = S _ { 矩形 O M C N } - S _ { \triangle A O M } - S _ { \triangle B O N } - S _ { \triangle A B C } = 3 \times 3 - \frac { 1 } { 2 } | k _ { 1 } | - \frac { 1 } { 2 } | k _ { 1 } | - \frac { 1 } { 2 } \times ( 3 - 1 ) \times ( 3 - 1 ) = 9 - \frac { 3 } { 2 } - \frac { 3 } { 2 } - 2 = 4 $。

14. (娄底娄星区二模)已知蓄电池的电压为定值,使用蓄电池时,电流 $ I ( \mathrm { A } ) $ 与电阻 $ R ( \Omega ) $ 是反比例函数关系,它的图象如图所示.下列说法正确的是()

A. 函数表达式为 $ I = \frac { 13 } { R } $
B. 蓄电池的电压是18V
C. 当 $ R = 6 \Omega $ 时, $ I = 4 \mathrm { A } $
D. 当 $ I \leq 10 \mathrm { A } $ 时, $ R \geq 3.6 \Omega $

答案： D

15. 实验数据显示,一般成人喝50mL某品牌白酒后,血液中酒精含量 $ y ( \mathrm { mg } / $ 百毫升)与时间 $ x ( \mathrm { h } ) $ 变化的图象如图(图象由线段OA与部分双曲线AB组成)所示.国家规定,车辆驾驶人员血液中的酒精含量大于或等于20mg/百毫升时属于“酒后驾驶”,不能驾车上路.
(1)求部分双曲线AB的表达式;
(2)参照上述数学模型,假设某驾驶员晚上22:00在家喝完50mL该品牌白酒,第二天早上6:30能否驾车去上班?请说明理由.

答案： 解：
(1) 设直线 OA 的表达式为 $ y = a x $。将点 $ \left( \frac { 1 } { 4 } , 20 \right) $ 代入，得 $ 20 = \frac { 1 } { 4 } a $，解得 $ a = 80 $，
∴ $ y = 80 x $。当 $ x = \frac { 3 } { 2 } $ 时，$ y = 80 \times \frac { 3 } { 2 } = 120 $，
∴ 点 $ A \left( \frac { 3 } { 2 } , 120 \right) $。设双曲线的表达式为 $ y = \frac { k } { x } $。将点 $ A \left( \frac { 3 } { 2 } , 120 \right) $ 代入，得 $ k = 180 $，
∴ $ y = \frac { 180 } { x } \left( x \geq \frac { 3 } { 2 } \right) $。
(2) 不能驾车去上班。理由如下：在 $ y = \frac { 180 } { x } $ 中，当 $ y = 20 $ 时，$ x = 9 $。从晚上 22:00 到第二天早上 6:30 时间间距为 8.5 h。$ \because 8.5 ＜ 9 $，
∴ 第二天早上 6:30 不能驾车去上班。