第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
9. 已知反比例函数$y= \frac {k}{x}(k≠0)$在每一个象限内,y随x的增大而增大,则下列各点可能在这个函数图象上的为()
A. $(2,3)$
B. $(-2,3)$
C. $(3,0)$
D. $(-3,-2)$
A. $(2,3)$
B. $(-2,3)$
C. $(3,0)$
D. $(-3,-2)$
答案:
B
10. 已知反比例函数$y= -\frac {12}{x}$,当$y≤4$时,自变量x的取值范围为()
A. $x≥3或x<0$
B. $x>0或x≤-3$
C. $x≤-3$
D. $x≥3$
A. $x≥3或x<0$
B. $x>0或x≤-3$
C. $x≤-3$
D. $x≥3$
答案:
B
11. (长沙天心区月考)如图是反比例函数$y_{1}= \frac {k_{1}}{x},y_{2}= \frac {k_{2}}{x},y_{3}= \frac {k_{3}}{x}$在x轴上方的图象,则$k_{1},k_{2},k_{3}$的大小关系为____.(用“<”连接)
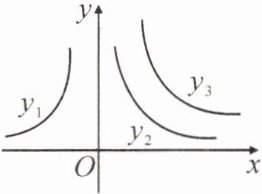

答案:
$k_{1}<k_{2}<k_{3}$
12. 已知$y= (m-2)x^{m^{2}-5}$是y关于x的反比例函数.
(1)函数图象的两个分支分别位于哪个象限? 在每个象限内,y随x的增大而怎样变化?
(2)当$-2≤x≤-1$时,y的取值范围为____.
(1)函数图象的两个分支分别位于哪个象限? 在每个象限内,y随x的增大而怎样变化?
(2)当$-2≤x≤-1$时,y的取值范围为____.
答案:
解:
(1)由题意,得$\left\{\begin{array}{l} m-2≠0,\\ m^{2}-5=-1,\end{array}\right. $解得$m=-2$,$\therefore$反比例函数的表达式为$y=-\frac {4}{x}$.$\because -4<0$,$\therefore$函数图象的两个分支分别位于第二、四象限,且在每个象限内,$y$随$x$的增大而增大.
(2)$2≤y≤4$
(1)由题意,得$\left\{\begin{array}{l} m-2≠0,\\ m^{2}-5=-1,\end{array}\right. $解得$m=-2$,$\therefore$反比例函数的表达式为$y=-\frac {4}{x}$.$\because -4<0$,$\therefore$函数图象的两个分支分别位于第二、四象限,且在每个象限内,$y$随$x$的增大而增大.
(2)$2≤y≤4$
13. 如图,点A,D分别在函数$y= -\frac {3}{x},y= \frac {6}{x}$的图象上,点B,C在x轴上.若四边形ABCD为正方形,点D在第一象限,求点D的坐标.
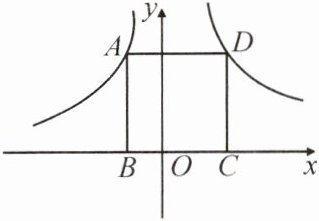

答案:
解:设点$A$的纵坐标为$n$,则点$D$的纵坐标为$n$.$\because$点$A$,$D$分别在函数$y=-\frac {3}{x}$,$y=\frac {6}{x}$的图象上,$\therefore A(-\frac {3}{n},n)$,$D(\frac {6}{n},n)$.$\because$四边形$ABCD$为正方形,$\therefore AD=CD$,即$\frac {6}{n}+\frac {3}{n}=n$,解得$n=3$(负值已舍去),$\therefore$点$D$的坐标为$(2,3)$.
14. (娄底双峰县期末)如图,在平面直角坐标系中,已知点$A(-2,0)$,过点A作y轴的平行线,交反比例函数$y= \frac {k}{x}$的图象于点B,$AB= \frac {3}{2}$.
(1)求反比例函数的表达式;
(2)若$P(x_{1},y_{1}),Q(x_{2},y_{2})$是该反比例函数图象上的两点,且当$x_{1}<x_{2}$时,$y_{1}>y_{2}$,指出点P,Q各位于哪个象限,并简要说明理由.
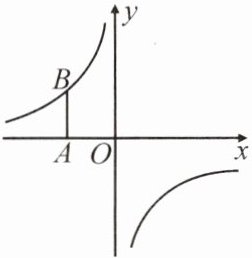
(1)求反比例函数的表达式;
(2)若$P(x_{1},y_{1}),Q(x_{2},y_{2})$是该反比例函数图象上的两点,且当$x_{1}<x_{2}$时,$y_{1}>y_{2}$,指出点P,Q各位于哪个象限,并简要说明理由.

答案:
解:
(1)由题意,得点$B$的坐标为$(-2,\frac {3}{2})$.把点$B(-2,\frac {3}{2})$代入$y=\frac {k}{x}$,得$k=-3$,$\therefore$反比例函数的表达式为$y=-\frac {3}{x}$.
(2)点$P$位于第二象限,点$Q$位于第四象限.理由如下:由
(1)知$k=-3<0$,$\therefore$在每个象限内,函数值$y$随$x$的增大而增大.$\because P(x_{1},y_{1})$,$Q(x_{2},y_{2})$是该反比例函数图象上的两点,且当$x_{1}<x_{2}$时,$y_{1}>y_{2}$,$\therefore$点$P$,$Q$在不同的象限,$\therefore$点$P$位于第二象限,点$Q$位于第四象限.
(1)由题意,得点$B$的坐标为$(-2,\frac {3}{2})$.把点$B(-2,\frac {3}{2})$代入$y=\frac {k}{x}$,得$k=-3$,$\therefore$反比例函数的表达式为$y=-\frac {3}{x}$.
(2)点$P$位于第二象限,点$Q$位于第四象限.理由如下:由
(1)知$k=-3<0$,$\therefore$在每个象限内,函数值$y$随$x$的增大而增大.$\because P(x_{1},y_{1})$,$Q(x_{2},y_{2})$是该反比例函数图象上的两点,且当$x_{1}<x_{2}$时,$y_{1}>y_{2}$,$\therefore$点$P$,$Q$在不同的象限,$\therefore$点$P$位于第二象限,点$Q$位于第四象限.
查看更多完整答案,请扫码查看


