《2025年课时夺冠九年级数学上册湘教版》

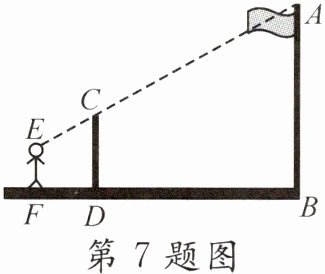
7. 九年级(1)班课外活动小组利用标杆CD测量学校旗杆AB的高度(标杆、旗杆均与地面垂直). 如图,已知标杆高度CD= 3m,标杆与旗杆的水平距离BD= 15m,人的眼睛与地面的高度EF= 1.6m,人与标杆CD的水平距离DF= 2m,人的眼睛E、标杆顶端C和旗杆顶端A在同一条直线上,则旗杆AB的高度为______m.

答案： 13.5

8. 如图,一条河的两岸有一段是平行的,在河的南岸边每隔5m有一棵树,在河的北岸边每隔50m有一根电线杆. 小丽站在离南岸15m的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有四棵树,则河的宽度为______m.

答案： 15

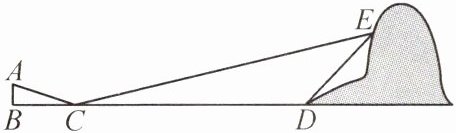
9. 如图,小华和同伴春游时,发现在某地小山坡的点E处有一棵小桃树,他们想利用皮尺、测倾器和平面镜测量小桃树E到山脚下的点D之间的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且测得BC= 6m,CD= 24m,∠CDE= 135°. 已知小华的身高AB= 1.5m,请根据以上数据,求DE的长度. (结果保留根号)

答案： 解：过点 $ E $ 作 $ EF \perp BC $ 于点 $ F $，$ \therefore \angle EFC = 90^{\circ} $。$ \because \angle CDE = 135^{\circ} $，$ \therefore \angle EDF = 45^{\circ} $，$ \therefore EF = DF $。设 $ EF = x \text{ m} $，则 $ DF = x \text{ m} $，$ \therefore DE = \sqrt{2}x \text{ m} $。$ \because \angle B = \angle EFC = 90^{\circ} $，$ \angle ACB = \angle ECF $，$ \therefore \triangle ABC \backsim \triangle EFC $，$ \therefore \frac{AB}{EF} = \frac{BC}{FC} $，即 $ \frac{1.5}{x} = \frac{6}{24 + x} $，解得 $ x = 8 $。经检验，$ x = 8 $ 是该分式方程的解，且符合题意，$ \therefore DE = 8\sqrt{2} \text{ m} $。答：$ DE $ 的长度为 $ 8\sqrt{2} \text{ m} $。

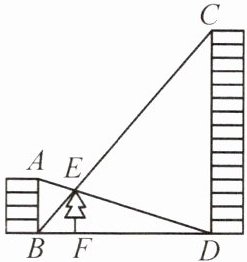
10. 如图,在高5m的房顶A处观望一幢楼的底部D,视线经过小树的顶端E,又从房底部B处观望楼顶C,视线也正好经过小树的顶端E,测得小树的高度EF为4m,求楼的高度CD.

答案： 解：$ \because EF // AB $，$ \therefore \triangle DEF \backsim \triangle DAB $，$ \therefore \frac{DF}{DB} = \frac{EF}{AB} = \frac{4}{5} $。$ \because EF // CD $，$ \therefore \triangle BEF \backsim \triangle BCD $，$ \therefore \frac{BF}{BD} = \frac{EF}{CD} = \frac{4}{CD} $。$ \because \frac{DF}{BD} + \frac{BF}{BD} = \frac{DF + BF}{BD} = 1 $，$ \therefore \frac{4}{5} + \frac{4}{CD} = 1 $，$ \therefore CD = 20 \text{ m} $。答：楼的高度 $ CD $ 为 $ 20 \text{ m} $。

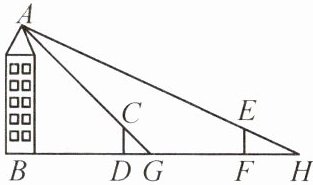
11. (衡阳石鼓区月考)如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高为2m的标杆CD和EF,两标杆相距52m,并且建筑物AB、标杆CD和EF在同一竖直平面内. 从标杆CD处后退2m到点G处,在点G处测得建筑物顶端A与标杆顶端C在同一条直线上；从标杆EF处后退4m到点H处,在点H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高度.

答案： 解：$ \because AB \perp BH $，$ CD \perp BH $，$ EF \perp BH $，$ \therefore \angle ABG = \angle CDG = \angle EFH = 90^{\circ} $。$ \because \angle CGD = \angle AGB $，$ \angle EHF = \angle AHB $，$ \therefore \triangle CDG \backsim \triangle ABG $，$ \triangle EFH \backsim \triangle ABH $，$ \therefore \frac{CD}{AB} = \frac{DG}{DG + BD} $，$ \frac{EF}{AB} = \frac{FH}{FH + DF + BD} $。由题意，得 $ CD = DG = EF = 2 \text{ m} $，$ DF = 52 \text{ m} $，$ FH = 4 \text{ m} $，$ \therefore \frac{2}{AB} = \frac{2}{2 + BD} $，$ \frac{2}{AB} = \frac{4}{4 + 52 + BD} $，$ \therefore \frac{2}{2 + BD} = \frac{4}{4 + 52 + BD} $，$ \therefore BD = 52 \text{ m} $，$ \therefore AB = 54 \text{ m} $。答：建筑物的高度为 $ 54 \text{ m} $。