《2025年课时夺冠九年级数学上册湘教版》

12. 如图,在菱形$ABCD$中,$E为边BC$上一点,$\angle AED= \angle B$.
(1)求证：$\triangle ABE\backsim\triangle DEA$；
(2)若$AB = 9$,求$AE\cdot DE$的值.

答案：
(1) 证明：
∵ 四边形 $ABCD$ 是菱形，
∴ $AD // BC$，
∴ $\angle AEB = \angle DAE$。
∵ $\angle B = \angle AED$，
∴ $\triangle ABE \backsim \triangle DEA$。
(2) 解：由
(1) 知 $\triangle ABE \backsim \triangle DEA$，
∴ $\frac{AE}{DA} = \frac{AB}{DE}$，
∴ $AE \cdot DE = AB \cdot DA$。
∵ 四边形 $ABCD$ 是菱形，
∴ $DA = AB = 9$，
∴ $AE \cdot DE = 9^2 = 81$。

13. 如图,在$\triangle ABC$中,点$D$,$E分别在边AB$,$BC$上,$BA\cdot BD = BC\cdot BE$.
(1)求证：$\triangle BDE\backsim\triangle BCA$；
(2)如果$AE = AC$,求证：$AC^2 = AD\cdot AB$.

答案： 证明：
(1)
∵ $BA \cdot BD = BC \cdot BE$，
∴ $\frac{BD}{BC} = \frac{BE}{BA}$。
∵ $\angle B = \angle B$，
∴ $\triangle BDE \backsim \triangle BCA$。
(2)
∵ $BA \cdot BD = BC \cdot BE$，
∴ $\frac{BD}{BE} = \frac{BC}{BA}$。
∵ $\angle B = \angle B$，
∴ $\triangle BAE \backsim \triangle BCD$，
∴ $\angle BAE = \angle BCD$。
∵ $AE = AC$，
∴ $\angle AEC = \angle ACE$。
∵ $\angle AEC = \angle B + \angle BAE$，$\angle ACE = \angle ACD + \angle BCD$，
∴ $\angle B = \angle ACD$。
∵ $\angle BAC = \angle CAD$，
∴ $\triangle ADC \backsim \triangle ACB$，
∴ $\frac{AD}{AC} = \frac{AC}{AB}$，
∴ $AC^2 = AD \cdot AB$。

14. (益阳安化县期末)如图,铁道口的栏杆短臂长$1\mathrm{m}$,长臂长$16\mathrm{m}$. 当短臂端点下降$0.5\mathrm{m}$时,长臂端点升高()

A. $5\mathrm{m}$
B. $6\mathrm{m}$
C. $7\mathrm{m}$
D. $8\mathrm{m}$

答案： D

15. 如图,某零件的外径为$10\mathrm{cm}$,用一个交叉卡钳(两条尺长$AC和BD$相等)可测量零件的内孔直径$AB$. 若$OA:OC = OB:OD = 3$,且量得$CD = 3\mathrm{cm}$,则零件的厚度$x$为()

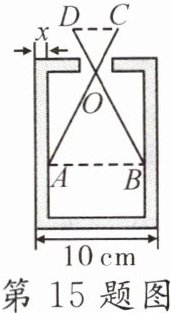
A. $0.3\mathrm{cm}$
B. $0.5\mathrm{cm}$
C. $0.7\mathrm{cm}$
D. $1\mathrm{cm}$

答案： B

16. (长沙一模)如图$1$是装了液体的高脚杯(数据如图),用去一部分液体后如图$2$所示,此时液面$AB$的宽度为()

A. $1\mathrm{cm}$
B. $2\mathrm{cm}$
C. $3\mathrm{cm}$
D. $4\mathrm{cm}$

答案： C

17. 如图,将一个装有水的杯子倾斜放置在水平桌面上,其截面可看作一个宽$BC = 6\mathrm{cm}$,长$CD = 16\mathrm{cm}$的矩形. 当水面触到杯口边缘时,边$CD$恰有一半露出水面,那么此时水面高度是()

A. $9.6\mathrm{cm}$
B. $9.3\mathrm{cm}$
C. $8.6\mathrm{cm}$
D. $7.2\mathrm{cm}$

答案： A

18. (株洲醴陵市月考)如图,在一块斜边长$30\mathrm{cm}$的直角三角形木板($\mathrm{Rt}\triangle ACB$)上截取一个正方形$CDEF$,点$D在边BC$上,点$E在斜边AB$上,点$F在边AC$上. 若$AF:AC = 1:3$,则这块木板截取正方形$CDEF$后,剩余部分的面积为____$\mathrm{cm}^2$.

答案： 100