《2025年课时夺冠九年级数学上册湘教版》

1. 反比例函数$y= \frac {2}{x}$的图象大致是()

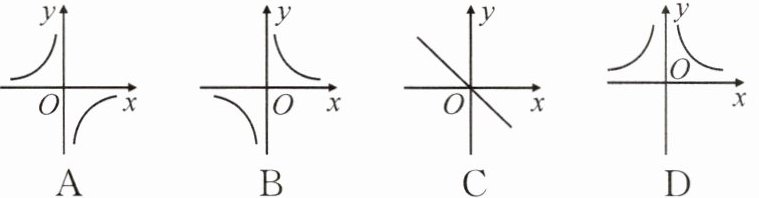
答案： B

2. 下列各点在反比例函数$y= \frac {16}{x}$的图象上的是()
A. $(1,-16)$
B. $(4,4)$
C. $(-2,8)$
D. $(-1,16)$

答案： B

3. (益阳安化县期末)已知反比例函数$y= \frac {3-4m}{x}$的图象经过第一、三象限,则m的取值范围为____.

答案： $m＜\frac{3}{4}$

4. 画出反比例函数$y= \frac {4}{x}$的图象.
(1)列表:(请将表格补充完整)

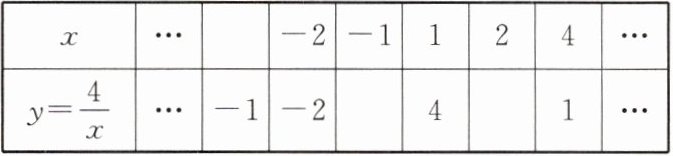
(2)描点连线.(请在所给的平面直角坐标系中画图)

答案：
解:
(1) $-4$ $-4$ $2$
(2) 如图所示.

5. 已知$A(1,y_{1}),B(2,y_{2})为反比例函数y= \frac {3}{x}$的图象上的两点,则$y_{1}与y_{2}$之间的大小关系是()
A. $y_{1}＞y_{2}$
B. $y_{1}＜y_{2}$
C. $y_{1}= y_{2}$
D. 无法确定

答案： A

6. 对于反比例函数$y= \frac {5}{x}$,下列说法中正确的是()
A. 随着自变量$x$的增大,函数值$y$也增大
B. 它的图象与$x$轴能够相交
C. 它的两支曲线与$y$轴都不相交
D. 它的图象关于$x$轴对称

答案： C

7. 已知反比例函数$y= \frac {12}{x}$,当$2＜x＜4$时,$y$的取值范围是____.

答案： $3＜y＜6$

8. 如图,已知反比例函数$y= \frac {k}{x}的图象经过点A(-3,-2)$.
(1)求反比例函数的表达式;
(2)若点$B(-1,m),C(-2,n)$在该函数的图象上,试比较$m与n$的大小.

答案： 解:
(1) $\because$ 反比例函数 $y=\frac{k}{x}$ 的图象经过点 $A(-3,-2), \therefore -2=\frac{k}{-3}, \therefore k=6, \therefore$ 反比例函数的表达式为 $y=\frac{6}{x}$.
(2) $\because$ 点 $B(-1,m), C(-2,n)$ 均在反比例函数 $y=\frac{6}{x}$ 位于第三象限的图象上，且 $-1＞-2, \therefore m＜n$.