《2025年课时夺冠九年级数学上册湘教版》

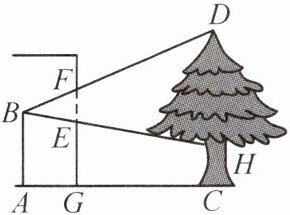
19. (常德石门县期末)如图,王老师为测得学校操场上小树$CD$的高,他站在教室里的点$A$处,从教室的窗口望出去,恰好能看见小树的整个树冠$DH$. 经测量,窗口高$EF = 1.4\mathrm{m}$,树干高$CH = 1.2\mathrm{m}$,$A$,$C$两点在同一水平线上,点$A距墙角点G\ 1.6\mathrm{m}$,点$C距墙角点G\ 4.8\mathrm{m}$,且$A$,$G$,$C$三点在同一条直线上. 请根据上面的信息,帮王老师计算出小树$CD$的高.

答案： 解：
∵ $FG \perp AC$，$DC \perp AC$，
∴ $FG // DC$，
∴ $\triangle BEF \backsim \triangle BHD$，
∴ $\frac{FE}{DH} = \frac{AG}{AC}$。
∵ $AG = 1.6\ \text{m}$，$CG = 4.8\ \text{m}$，$EF = 1.4\ \text{m}$，
∴ $\frac{1.4}{DH} = \frac{1.6}{1.6 + 4.8}$，解得 $DH = 5.6$，
∴ 小树 $CD$ 的高为 $DH + CH = 5.6 + 1.2 = 6.8(\text{m})$。

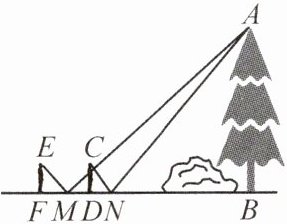
20. (邵阳模拟)“创新实践”小组想利用镜子与皮尺测量大树$AB$的高度,因大树底部有障碍物,无法直接测量到大树底部的距离. 聪明的小颖设计出如图所示的测量方案：测量者站在点$F$处,将镜子放在点$M$处时,刚好看到大树的顶端,沿大树方向向前走$2.8\mathrm{m}到达点D$处,将镜子放在点$N$处时,刚好看到大树的顶端(点$F$,$M$,$D$,$N$,$B$在同一条直线上). 若测得$FM = 1.5\mathrm{m}$,$DN = 1.1\mathrm{m}$,测量者眼睛到地面的距离为$1.6\mathrm{m}$,求大树$AB$的高度.

答案： 解：设 $BN$ 的长为 $x\ \text{m}$，则 $BM = x + 1.1 + 2.8 - 1.5 = x + 2.4(\text{m})$。由题意，得 $\angle CND = \angle ANB$，$\angle CDN = \angle ABN = 90^\circ$，
∴ $\triangle CND \backsim \triangle ANB$，
∴ $\frac{CD}{AB} = \frac{DN}{BN}$。同理 $\triangle EMF \backsim \triangle AMB$，
∴ $\frac{EF}{AB} = \frac{FM}{BM}$。
∵ $EF = CD$，
∴ $\frac{DN}{BN} = \frac{FM}{BM}$，即 $\frac{1.1}{x} = \frac{1.5}{x + 2.4}$，解得 $x = 6.6$。
∵ $\frac{CD}{AB} = \frac{DN}{BN}$，
∴ $\frac{1.6}{AB} = \frac{1.1}{6.6}$，解得 $AB = 9.6$。答：大树 $AB$ 的高度为 $9.6\ \text{m}$。

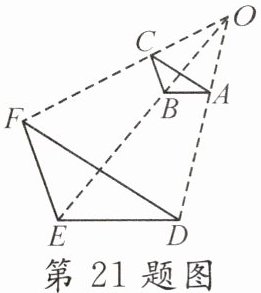
21. 如图,$\triangle ABC和\triangle DEF是以点O$为位似中心的位似图形,$OA:OD = 2:5$,$\triangle ABC的周长为8$,则$\triangle DEF$的周长为()

A. $12$
B. $18$
C. $20$
D. $30$

答案： C

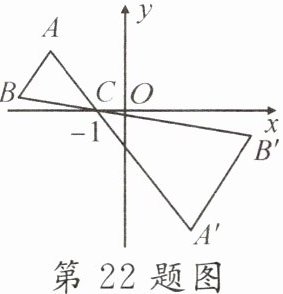
22. 如图,在$\triangle ABC$中,$A$,$B两个顶点在x$轴的上方,点$C的坐标为(-1,0)$,以点$C$为位似中心,将$\triangle ABC放大为原来的2$倍,在$x轴的下方作\triangle ABC的位似图形\triangle A'B'C$. 设点$B的横坐标是m$,则点$B'$的横坐标是____.

答案： $-2m - 3$

23. 如图,$\triangle OAB的顶点坐标分别为O(0,0)$,$A(2,1)$,$B(1,-2)$.
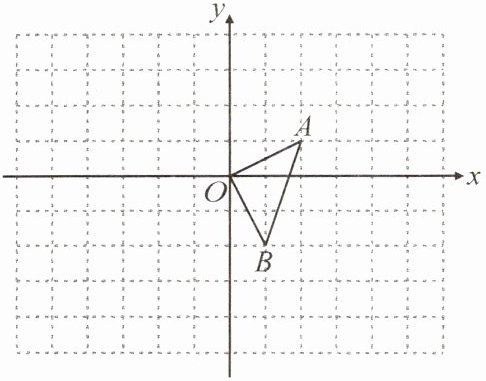
(1)以原点$O$为位似中心,在$y轴的右侧画出\triangle OAB的位似三角形OA_1B_1$,使它与$\triangle OAB的位似比为2:1$,并写出点$A的对应点A_1$的坐标；
(2)画出将$\triangle OAB向左平移2$个单位长度,再向上平移$1个单位长度后的\triangle O_2A_2B_2$,并写出点$A_2$的坐标；
(3)判断$\triangle OA_1B_1与\triangle O_2A_2B_2是否是关于某一点M$为位似中心的位似图形？若是,请在图中标出位似中心点$M$,并写出点$M$的坐标.

答案： 解：
(1) 图略，点 $A_1(4, 2)$。
(2) 图略，点 $A_2(0, 2)$。
(3) $\triangle OA_1B_1$ 与 $\triangle O_2A_2B_2$ 是关于点 $M(-4, 2)$ 为位似中心的位似图形。