《2025年课时夺冠九年级数学上册湘教版》

1. 如图,为估算某河的宽度,在河对岸岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上. 若测得BE= 20m,EC= 10m,CD= 20m,则河的宽度AB为()

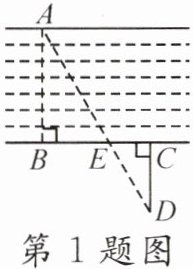
A. 60m
B. 40m
C. 30m
D. 20m

答案： B

2. (怀化会同县期末)如图,A,B两点被池塘隔开,在AB外取一点C,连接AC,BC,在AC上取点M,使AM= 3MC,作MN//AB交BC于点N,量得MN= 38m,则AB的长为______m.

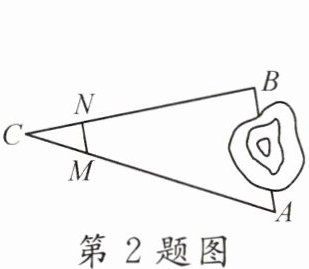
答案： 152

3. 如图,测量小玻璃管口径的量具ABC,AB的长为10cm,AC被分为60等份. 如果小玻璃管口DE正好对着量具上20等份处,且DE//AB,求小玻璃管口径DE的宽.

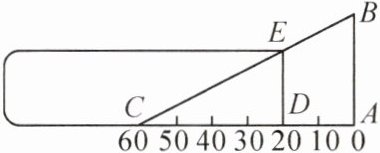
答案： 解：由题意，得 $ CD = 60 - 20 = 40(\text{cm}) $，$ AC = 60 \text{ cm} $。$ \because DE // AB $，$ \therefore \triangle CDE \backsim \triangle CAB $，$ \therefore \frac{DE}{AB} = \frac{CD}{CA} $，即 $ \frac{DE}{10} = \frac{40}{60} $，解得 $ DE = \frac{20}{3} \text{ cm} $。答：小玻璃管口径 $ DE $ 的宽是 $ \frac{20}{3} \text{ cm} $。

4. 如图,某校数学兴趣小组的同学利用标杆BE测量建筑物CD的高度. 已知标杆BE的高为1.5m,测得AB= 1.2m,BC= 12.8m,则建筑物CD的高为()

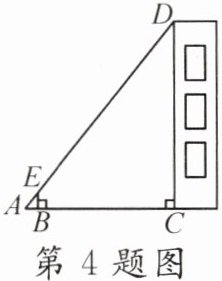
A. 17.5m
B. 17m
C. 16.5m
D. 18m

答案： A

5. 为了测量校园内一棵大树AB的高度,学校数学兴趣小组做了如下的探索：根据光的反射定律,利用一面镜子和一根皮尺,设计了如图所示的测量方案：把一面很小的镜子放在离树底B约8.4m的E处,然后沿着直线BE后退到点D处,这时恰好在镜子中看到树梢顶点A,再用皮尺量得DE= 2.4m,观察者身高CD= 1.6m,则树AB的高度约为______m.

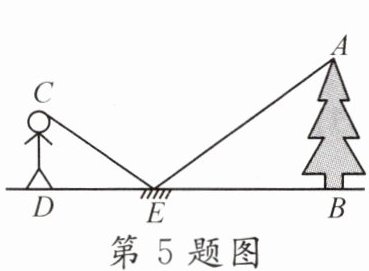
答案： 5.6

6. 如图,小明同学用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,使斜边DF保持水平,且边DE与点B在同一条直线上. 已知DE= 0.4m,EF= 0.2m,测得边DF距离地面的高度AC= 1.5m,CD= 8m,求树AB的高.

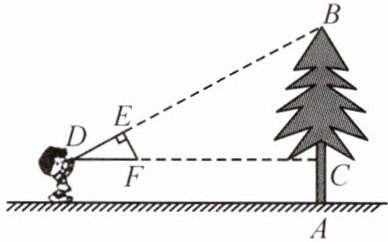
答案： 解：$ \because \angle DEF = \angle DCB = 90^{\circ} $，$ \angle D = \angle D $，$ \therefore \triangle DEF \backsim \triangle DCB $，$ \therefore \frac{DE}{DC} = \frac{EF}{CB} $，即 $ \frac{0.4}{8} = \frac{0.2}{CB} $，解得 $ CB = 4 $，$ \therefore AB = AC + CB = 1.5 + 4 = 5.5(\text{m}) $。答：树 $ AB $ 的高为 $ 5.5 \text{ m} $。