第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
9. 如果一个直角三角形的两条边长分别为6和8,另一个与它相似的直角三角形的三条边长分别为3,4及x,那么x的值()
A. 只有1个
B. 可以有2个
C. 可以有3个
D. 有无数个
A. 只有1个
B. 可以有2个
C. 可以有3个
D. 有无数个
答案:
B
10. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,要使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似,则“马”应落在()
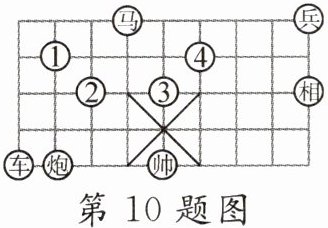
A. ①处
B. ②处
C. ③处
D. ④处

A. ①处
B. ②处
C. ③处
D. ④处
答案:
B
11. 如图,四边形ABCD的顶点在正方形网格线的交点上,则$∠BDC$的度数为____.
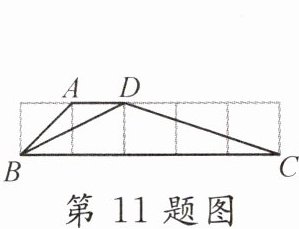

答案:
$135^{\circ}$
12. 如图,已知$AB// A'B',\frac {B'C'}{BC}= \frac {OB'}{OB},\frac {A'C'}{AC}= \frac {OA'}{OA}$,求证:$\triangle ABC\backsim \triangle A'B'C'.$
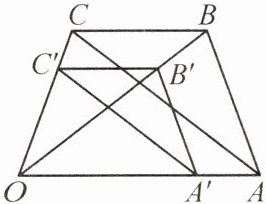

答案:
证明:$\because AB // A'B'$,$\therefore \triangle OA'B' \backsim \triangle OAB$,$\therefore \frac{A'B'}{AB} = \frac{OB'}{OB} = \frac{OA'}{OA}$. $\because \frac{B'C'}{BC} = \frac{OB'}{OB}$,$\frac{A'C'}{AC} = \frac{OA'}{OA}$,$\therefore \frac{A'B'}{AB} = \frac{B'C'}{BC} = \frac{A'C'}{AC}$,$\therefore \triangle ABC \backsim \triangle A'B'C'$.
13. 如图,在四边形ABCD中,AC,BD相交于点F,点E在BD上,且$\frac {AB}{AE}= \frac {BC}{ED}= \frac {AC}{AD}$.
(1)$∠1与∠2$相等吗? 为什么?
(2)判断$\triangle ABE与\triangle ACD$是否相似,并说明理由.
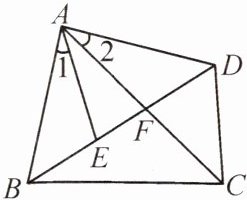
(1)$∠1与∠2$相等吗? 为什么?
(2)判断$\triangle ABE与\triangle ACD$是否相似,并说明理由.

答案:
解:
(1) $\angle 1$与$\angle 2$相等. 理由如下:$\because \frac{AB}{AE} = \frac{BC}{ED} = \frac{AC}{AD}$,$\therefore \triangle ABC \backsim \triangle AED$,$\therefore \angle BAC = \angle EAD$,$\therefore \angle BAC - \angle EAF = \angle EAD - \angle EAF$,即$\angle 1 = \angle 2$.
(2) $\triangle ABE$与$\triangle ACD$相似. 理由如下:$\because \frac{AB}{AE} = \frac{AC}{AD}$,$\therefore \frac{AB}{AC} = \frac{AE}{AD}$. 由
(1)知$\angle 1 = \angle 2$,$\therefore \triangle ABE \backsim \triangle ACD$.
(1) $\angle 1$与$\angle 2$相等. 理由如下:$\because \frac{AB}{AE} = \frac{BC}{ED} = \frac{AC}{AD}$,$\therefore \triangle ABC \backsim \triangle AED$,$\therefore \angle BAC = \angle EAD$,$\therefore \angle BAC - \angle EAF = \angle EAD - \angle EAF$,即$\angle 1 = \angle 2$.
(2) $\triangle ABE$与$\triangle ACD$相似. 理由如下:$\because \frac{AB}{AE} = \frac{AC}{AD}$,$\therefore \frac{AB}{AC} = \frac{AE}{AD}$. 由
(1)知$\angle 1 = \angle 2$,$\therefore \triangle ABE \backsim \triangle ACD$.
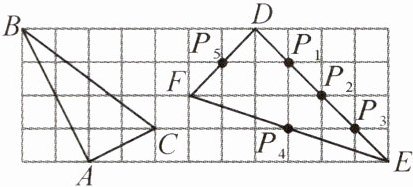
14. (怀化溆浦县月考)如图,在边长为1的小正方形组成的网格中,$\triangle ABC和\triangle DEF$的顶点都在格点上,$P_{1},P_{2},P_{3},P_{4},P_{5}是\triangle DEF$边上的5个格点,请按要求完成下列各题:
(1)判断$\triangle ABC和\triangle DEF$是否相似,并说明理由;
(2)画一个三角形,使它的三个顶点为$P_{1},P_{2},P_{3},P_{4},P_{5}$中的3个格点并且与$\triangle ABC$相似(不要求写证明过程).
(1)判断$\triangle ABC和\triangle DEF$是否相似,并说明理由;
(2)画一个三角形,使它的三个顶点为$P_{1},P_{2},P_{3},P_{4},P_{5}$中的3个格点并且与$\triangle ABC$相似(不要求写证明过程).

答案:
解:
(1) $\triangle ABC$和$\triangle DEF$相似,理由如下:根据勾股定理,得$AB = 2\sqrt{5}$,$AC = \sqrt{5}$,$BC = 5$;$DE = 4\sqrt{2}$,$DF = 2\sqrt{2}$,$EF = 2\sqrt{10}$,$\therefore \frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF} = \frac{\sqrt{10}}{4}$,$\therefore \triangle ABC \backsim \triangle DEF$.
(2) 连接$P_2P_5$,$P_2P_4$,$P_4P_5$,则$\triangle ABC \backsim \triangle P_4P_5P_2$.
(1) $\triangle ABC$和$\triangle DEF$相似,理由如下:根据勾股定理,得$AB = 2\sqrt{5}$,$AC = \sqrt{5}$,$BC = 5$;$DE = 4\sqrt{2}$,$DF = 2\sqrt{2}$,$EF = 2\sqrt{10}$,$\therefore \frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF} = \frac{\sqrt{10}}{4}$,$\therefore \triangle ABC \backsim \triangle DEF$.
(2) 连接$P_2P_5$,$P_2P_4$,$P_4P_5$,则$\triangle ABC \backsim \triangle P_4P_5P_2$.
查看更多完整答案,请扫码查看


