《2025年课时夺冠九年级数学上册湘教版》

7. 某电商对一款成本价为每件40元的小商品进行直播销售.如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品的售价每降低5元,日销售量增加10件.
(1)若日利润保持不变,商家想尽快销售完该商品,每件售价应定为多少元?
(2)小明的线下实体商店也销售同款小商品,标价为每件62.5元.为促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?

答案： 解：
(1)设每件售价为$x$元，则每件的利润为$(x - 40)$元，日销售量为$20 + \frac{10(60 - x)}{5} = 140 - 2x$(件)。由题意，得$(x - 40)(140 - 2x) = (60 - 40)×20$，解得$x_1 = 50$，$x_2 = 60$。
∵要尽快销售完该商品，
∴$x = 50$。答：每件售价应定为50元。
(2)设该商品打$a$折销售。由题意，得$62.5×\frac{a}{10} ≤ 50$，解得$a ≤ 8$。答：该商品至少需打八折销售。

8. 某水果店标价为10元/kg的某种水果经过两次降价后,价格为8.1元/kg,且两次降价的百分率相同.
(1)求该水果每次降价的百分率;
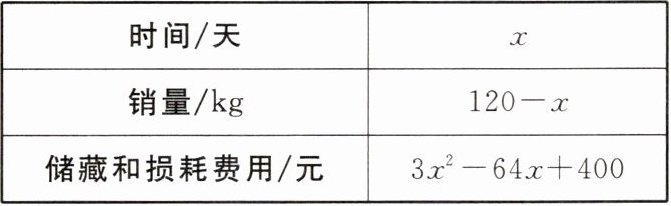
(2)设从第二次降价的第1天算起,第x天(x为整数)的销量及储藏和损耗费用的相关信息如下表所示.已知该水果的进价为4.1元/kg,设销售该水果第x天$(1≤x＜10)$天的利润为368元,求x的值.

答案： 解：
(1)设该水果每次降价的百分率为$m$。依题意，得$10(1 - m)^2 = 8.1$，解得$m_1 = 0.1 = 10\%$，$m_2 = 1.9$(不合题意，舍去)。答：该水果每次降价的百分率为10%。
(2)依题意，得$(8.1 - 4.1)(120 - x) - (3x^2 - 64x + 400) = 368$，整理，得$x^2 - 20x + 96 = 0$，解得$x_1 = 8$，$x_2 = 12$。
∵$1 ≤ x ＜ 10$，
∴$x = 8$。

9. (怀化合同县期中)为满足市场需求,某超市在端午节前夕购进价格为3元/个的粽子.根据市场调查发现,当该品牌粽子售价为4元/个时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个.为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的200%.
(1)当该品牌每个粽子的售价为多少元时,超市每天销售该品牌粽子的利润为800元?
(2)超市每天销售该品牌粽子的利润能否达到1000元?若能,请求出该品牌每个粽子的售价;若不能,请说明理由.

答案： 解：
(1)设当每个粽子的售价为$x$元时，超市每天销售该品牌粽子的利润为800元。由题意，得$(x - 3)(500 - 10×\frac{x - 4}{0.1}) = 800$。整理，得$x^2 - 12x + 35 = 0$，解得$x_1 = 7$，$x_2 = 5$。
∵售价不能超过进价的200%，
∴$x ≤ 3×200\%$，即$x ≤ 6$，
∴$x = 5$。答：当该品牌每个粽子的售价为5元时，超市每天销售该品牌粽子的利润为800元。
(2)不能。理由如下：设当每个粽子的售价为$y$元时，超市每天销售该品牌粽子的利润为1000元。由题意，得$(y - 3)(500 - 10×\frac{y - 4}{0.1}) = 1000$。整理，得$y^2 - 12y + 37 = 0$，$\Delta = (- 12)^2 - 4×1×37 = - 4 ＜ 0$，
∴该方程没有实数根，
∴超市每天销售该品牌粽子的利润不能达到1000元。