《2025年课时夺冠九年级数学上册湘教版》

9. (娄底双峰县期中)如图,在$\triangle ABC$中,$\angle A = 78^{\circ}$,$AB = 4$,$AC = 6$. 将$\triangle ABC$沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是()

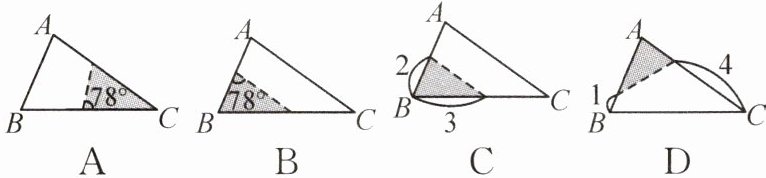
答案： C

10. 如图,在$\triangle ABC$中,$D为BC$上一点,$BC = \sqrt{3}AB = 3BD$,则$\frac{AD}{AC}$的值为______.

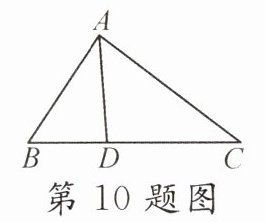
答案： $ \frac{\sqrt{3}}{3} $

11. 在$\triangle ABC$中,$AB = 6$,$AC = 5$,点$D在边AB$上,且$AD = 2$,点$E在边AC$上,当$AE$的长为______时,以$A$,$D$,$E为顶点的三角形与\triangle ABC$相似.

答案： $ \frac{12}{5} $ 或 $ \frac{5}{3} $

12. 如图,在$\triangle ABC$中,$\angle B = 90^{\circ}$,$AB = 4$,$BC = 2$,以$AC为边作等腰直角三角形ACE$,$\angle ACE = 90^{\circ}$,延长$BC至点D$,使$CD = 5$,连接$DE$. 求证：$\triangle ABC \backsim \triangle CED$.

答案： 证明：$ \because \angle B = 90^{\circ} $，$ AB = 4 $，$ BC = 2 $，$ \therefore AC = \sqrt{2^{2} + 4^{2}} = 2\sqrt{5} $. $ \because CE = AC $，$ \therefore CE = 2\sqrt{5} $. $ \because \frac{AB}{CE} = \frac{4}{2\sqrt{5}} = \frac{2\sqrt{5}}{5} $，$ \frac{AC}{CD} = \frac{2\sqrt{5}}{5} $，$ \therefore \frac{AB}{CE} = \frac{AC}{CD} $. $ \because \angle B = 90^{\circ} $，$ \angle ACE = 90^{\circ} $，$ \therefore \angle BAC + \angle BCA = 90^{\circ} $，$ \angle BCA + \angle ECD = 90^{\circ} $，$ \therefore \angle BAC = \angle ECD $，$ \therefore \triangle ABC \backsim \triangle CED $.

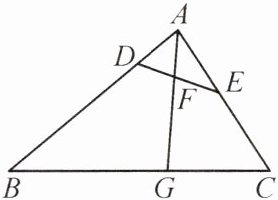
13. 如图,在$\triangle ABC$中,点$D$,$E分别在边AB$,$AC$上,$\angle AED = \angle B$,射线$AG分别交线段DE$,$BC于点F$,$G$,且$\frac{AD}{AC} = \frac{DF}{CG}$.
(1)求证：$\triangle ADF \backsim \triangle ACG$；
(2)若$\frac{AD}{AC} = \frac{1}{3}$,求$\frac{AF}{FG}$的值.

答案：
(1) 证明：$ \because \angle AED = \angle B $，$ \angle DAE = \angle CAB $，$ \therefore \angle ADF = \angle C $. 又 $ \because \frac{AD}{AC} = \frac{DF}{CG} $，$ \therefore \triangle ADF \backsim \triangle ACG $.
(2) 解：由
(1) 知 $ \triangle ADF \backsim \triangle ACG $，$ \therefore \frac{AD}{AC} = \frac{AF}{AG} $. 又 $ \because \frac{AD}{AC} = \frac{1}{3} $，$ \therefore \frac{AF}{AG} = \frac{1}{3} $，$ \therefore \frac{AF}{FG} = \frac{AF}{AG - AF} = \frac{1}{2} $.

14. (娄底新化县期末)如图,$AB // CD$,$AC与BD相交于点E$,且$\angle ACB = 90^{\circ}$,$AB = 6\sqrt{5}$,$BC = 6$,$CE = 3$.
(1)求$CD$的长；
(2)求证：$\triangle CDE \backsim \triangle BDC$.

答案：
(1) 解：$ \because \angle ACB = 90^{\circ} $，$ \therefore AC = \sqrt{AB^{2} - BC^{2}} = 12 $，$ \therefore AE = AC - CE = 9 $. $ \because AB // CD $，$ \therefore \triangle CDE \backsim \triangle ABE $，$ \therefore \frac{CD}{AB} = \frac{CE}{AE} $，$ \therefore CD = \frac{AB \cdot CE}{AE} = \frac{6\sqrt{5} \times 3}{9} = 2\sqrt{5} $.
(2) 证明：$ \because \angle ACB = 90^{\circ} $，$ \therefore BE = \sqrt{CE^{2} + BC^{2}} = 3\sqrt{5} $. $ \because AB // CD $，$ \therefore \frac{DE}{BE} = \frac{CE}{AE} = \frac{3}{9} = \frac{1}{3} $，$ \therefore DE = \sqrt{5} $，$ \therefore BD = DE + BE = 4\sqrt{5} $. $ \because \frac{DE}{CD} = \frac{\sqrt{5}}{2\sqrt{5}} = \frac{1}{2} $，$ \frac{CD}{BD} = \frac{2\sqrt{5}}{4\sqrt{5}} = \frac{1}{2} $，$ \therefore \frac{DE}{CD} = \frac{CD}{BD} $. $ \because \angle D = \angle D $，$ \therefore \triangle CDE \backsim \triangle BDC $.