第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
12. 已知$∠A$为锐角,且满足$|\sqrt {3}-2sinA|= 0$,则$cosA$的值为()
A. $\frac {1}{2}$
B. $\frac {\sqrt {2}}{2}$
C. $\frac {\sqrt {3}}{2}$
D. 1
A. $\frac {1}{2}$
B. $\frac {\sqrt {2}}{2}$
C. $\frac {\sqrt {3}}{2}$
D. 1
答案:
A
13. 在等腰三角形$ABC$中,$AB= AC= 10$,$BC= 12$,则$cos\frac {A}{2}$的值是()
A. $\frac {3}{5}$
B. $\frac {4}{5}$
C. $\frac {3}{4}$
D. $\frac {5}{4}$
A. $\frac {3}{5}$
B. $\frac {4}{5}$
C. $\frac {3}{4}$
D. $\frac {5}{4}$
答案:
B
14. 如图,在$△ABC$中,$∠C= 90^{\circ }$,点$D在BC$上,$BD= 6$,$AD= BC$,$cos∠ADC= \frac {3}{5}$,则$CD$的长为()
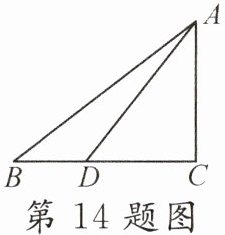
A. 9
B. 15
C. 3
D. 6

A. 9
B. 15
C. 3
D. 6
答案:
A
15. 如图,小正方形的边长均为1,点$A$,$B$,$C$都在格点上,则$∠ABC$的余弦值是______。
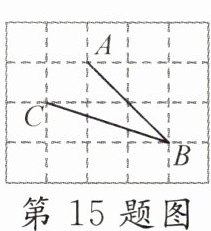

答案:
$\frac{2\sqrt{5}}{5}$
16. 如图,在$//ogram ABCD$中,$AB⊥AC$。已知$AB= 10\sqrt {6}$,$//ogram ABCD的面积为200\sqrt {3}$。
(1)求$cosD$的值;
(2)求$∠BAD$的度数。
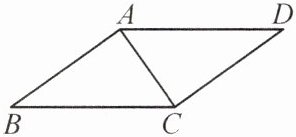
(1)求$cosD$的值;
(2)求$∠BAD$的度数。

答案:
解:(1)$\because AB \perp AC$,$\therefore S_{\square ABCD} = AB \cdot AC = 10\sqrt{6}AC = 200\sqrt{3}$,$\therefore AC = 10\sqrt{2}$,$\therefore BC = \sqrt{AB^{2} + AC^{2}} = 20\sqrt{2}$。$\because$ 四边形$ABCD$是平行四边形,$\therefore \angle B = \angle D$,$\therefore \cos D = \cos B = \frac{AB}{BC} = \frac{\sqrt{3}}{2}$。(2)由(1)知$\cos D = \frac{\sqrt{3}}{2}$,$\therefore \angle D = 30^{\circ}$。$\because$ 四边形$ABCD$是平行四边形,$\therefore AB // CD$,$\therefore \angle BAD = 180^{\circ} - \angle D = 150^{\circ}$。
17. (永州新田县期末)如图,在平面直角坐标系中,$O$为原点,点$A的坐标为(10,0)$,点$B$在第一象限,$BO= 5$,$cos∠BOA= \frac {4}{5}$。
(1)求点$B$的坐标;
(2)求$cos∠BAO$的值。
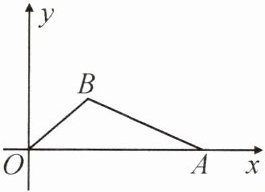
(1)求点$B$的坐标;
(2)求$cos∠BAO$的值。

答案:
解:(1)过点$B$作$BH \perp OA$于点$H$,$\therefore \angle BHO = 90^{\circ}$。在$Rt\triangle BOH$中,$\cos \angle BOA = \frac{OH}{OB} = \frac{4}{5}$,$\therefore \frac{OH}{5} = \frac{4}{5}$,$\therefore OH = 4$,$\therefore BH = \sqrt{OB^{2} - OH^{2}} = 3$,$\therefore$ 点$B$的坐标为$(4, 3)$。(2)由(1)知$OH = 4$,$BH = 3$。$\because$ 点$A$的坐标为$(10, 0)$,$\therefore OA = 10$,$\therefore AH = OA - OH = 6$。$\because BH \perp OA$,$\therefore \angle BHA = 90^{\circ}$,$\therefore$ 在$Rt\triangle BHA$中,$AB = \sqrt{BH^{2} + AH^{2}} = 3\sqrt{5}$,$\therefore \cos \angle BAO = \frac{AH}{AB} = \frac{6}{3\sqrt{5}} = \frac{2\sqrt{5}}{5}$。
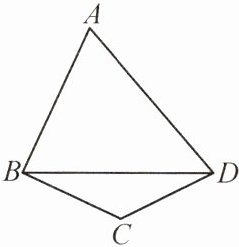
18. (张家界永定区期末)如图,在四边形$ABCD$中,$∠ABC= 90^{\circ }$,$AD= BD$,$BC= CD$。
(1)若$BD= 13$,$AB= 10$,求$cos∠CBD$的值;
(2)设$△ABD的面积为S_{1}$,$△BCD的面积为S_{2}$,求证:$\frac {S_{1}}{S_{2}}= 4cos^{2}∠CBD$。
(1)若$BD= 13$,$AB= 10$,求$cos∠CBD$的值;
(2)设$△ABD的面积为S_{1}$,$△BCD的面积为S_{2}$,求证:$\frac {S_{1}}{S_{2}}= 4cos^{2}∠CBD$。

答案:
(1)解:过点$D$作$DE \perp AB$于点$E$,$\therefore \angle AED = 90^{\circ} = \angle ABC$,$\therefore DE // BC$,$\therefore \angle CBD = \angle BDE$。$\because BD = AD$,$\therefore BE = AE = \frac{1}{2}AB = 5$。在$Rt\triangle BED$中,$DE = \sqrt{BD^{2} - BE^{2}} = \sqrt{13^{2} - 5^{2}} = 12$,$\therefore \cos \angle CBD = \cos \angle BDE = \frac{DE}{DB} = \frac{12}{13}$。
(2)证明:过点$C$作$CF \perp BD$于点$F$,$\therefore \angle BFC = 90^{\circ}$。$\because DE \perp AB$,$\therefore \angle BED = 90^{\circ} = \angle BFC$。$\because BC = CD$,$\therefore BD = 2BF$。由(1)知$\angle CBD = \angle BDE$,$\therefore \triangle DEB \sim \triangle BFC$,$\therefore \frac{S_{1}}{S_{2}} = (\frac{DE}{BF})^{2} = 4 \times (\frac{DE}{2BF})^{2} = 4 \times (\frac{DE}{DB})^{2}$。由(1)知$\cos \angle CBD = \frac{DE}{DB}$,$\therefore \frac{S_{1}}{S_{2}} = 4\cos^{2} \angle CBD$。
(2)证明:过点$C$作$CF \perp BD$于点$F$,$\therefore \angle BFC = 90^{\circ}$。$\because DE \perp AB$,$\therefore \angle BED = 90^{\circ} = \angle BFC$。$\because BC = CD$,$\therefore BD = 2BF$。由(1)知$\angle CBD = \angle BDE$,$\therefore \triangle DEB \sim \triangle BFC$,$\therefore \frac{S_{1}}{S_{2}} = (\frac{DE}{BF})^{2} = 4 \times (\frac{DE}{2BF})^{2} = 4 \times (\frac{DE}{DB})^{2}$。由(1)知$\cos \angle CBD = \frac{DE}{DB}$,$\therefore \frac{S_{1}}{S_{2}} = 4\cos^{2} \angle CBD$。
查看更多完整答案,请扫码查看


