第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
7. 小伟用撬棍撬动一块大石头,已知阻力和阻力臂分别为 1000 N 和 0.6 m,当动力臂由 1.5 m 增加到 2 m 时,撬动这块石头可以节省______N 的力.(杠杆原理:阻力×阻力臂= 动力×动力臂)
答案:
$ 100 $
8. 物理学中有这样的事实:当压力 F 不变时,压强 p 和受力面积 S 之间是反比例函数关系,可以表示成 $ p = \frac { F } { S } $.如图,一个圆台形物体的上底面面积是下底面面积的 $ \frac { 2 } { 3 } $,如果正放在桌面上,对桌面的压强是 200 Pa,那么翻过来放,对桌面的压强是______Pa.
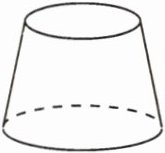

答案:
$ 300 $
9. 一辆客车从甲地出发前往乙地,平均速度 $ v ( km / h ) $与所用时间 $ t ( h ) $的函数关系如图所示,其中 $ 60 \leq v \leq 120 $.
(1)求 v 与 t 之间的函数表达式及 t 的取值范围;
(2)客车上午 8 时从甲地出发.
①客车需在当天 14 时 40 分至 15 时 30 分(含 14 时 40 分与 15 时 30 分)之间到达乙地,求客车行驶速度 v 的取值范围;
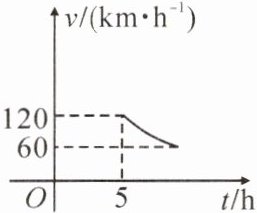
②客车能否在当天 12 时 30 分前到达乙地?请说明理由.
(1)求 v 与 t 之间的函数表达式及 t 的取值范围;
(2)客车上午 8 时从甲地出发.
①客车需在当天 14 时 40 分至 15 时 30 分(含 14 时 40 分与 15 时 30 分)之间到达乙地,求客车行驶速度 v 的取值范围;

②客车能否在当天 12 时 30 分前到达乙地?请说明理由.
答案:
解:
(1)设 $ v $ 与 $ t $ 之间的函数表达式为 $ v = \frac{k}{t} $。将点 $ (5, 120) $ 代入 $ v = \frac{k}{t} $,得 $ 120 = \frac{k}{5} $,解得 $ k = 600 $,$\therefore v $ 与 $ t $ 之间的函数表达式为 $ v = \frac{600}{t} $。当 $ v = 60 $ 时,$ 60 = \frac{600}{t} $,解得 $ t = 10 $,$\therefore t $ 的取值范围为 $ 5 \leq t \leq 10 $。
(2)① $ 14 $ 时 $ 40 $ 分 $ - 8 $ 时 $ = \frac{20}{3}(\mathrm{h}) $,$ 15 $ 时 $ 30 $ 分 $ - 8 $ 时 $ = \frac{15}{2}(\mathrm{h}) $。当 $ t = \frac{20}{3} $ 时,$ v = \frac{600}{t} = 600 \div \frac{20}{3} = 90 $,当 $ t = \frac{15}{2} $ 时,$ v = \frac{600}{t} = 600 \div \frac{15}{2} = 80 $,$\therefore $ 客车行驶速度 $ v $ 的取值范围为 $ 80 \mathrm{km/h} \leq v \leq 90 \mathrm{km/h} $。②不能。理由如下:$ 12 $ 时 $ 30 $ 分 $ - 8 $ 时 $ = \frac{9}{2}(\mathrm{h}) $,当 $ t = \frac{9}{2} $ 时,$ v = \frac{600}{t} = 600 \div \frac{9}{2} \approx 133 $。$\because 133 > 120 $,$\therefore $ 客车不能在当天 $ 12 $ 时 $ 30 $ 分前到达乙地。
(1)设 $ v $ 与 $ t $ 之间的函数表达式为 $ v = \frac{k}{t} $。将点 $ (5, 120) $ 代入 $ v = \frac{k}{t} $,得 $ 120 = \frac{k}{5} $,解得 $ k = 600 $,$\therefore v $ 与 $ t $ 之间的函数表达式为 $ v = \frac{600}{t} $。当 $ v = 60 $ 时,$ 60 = \frac{600}{t} $,解得 $ t = 10 $,$\therefore t $ 的取值范围为 $ 5 \leq t \leq 10 $。
(2)① $ 14 $ 时 $ 40 $ 分 $ - 8 $ 时 $ = \frac{20}{3}(\mathrm{h}) $,$ 15 $ 时 $ 30 $ 分 $ - 8 $ 时 $ = \frac{15}{2}(\mathrm{h}) $。当 $ t = \frac{20}{3} $ 时,$ v = \frac{600}{t} = 600 \div \frac{20}{3} = 90 $,当 $ t = \frac{15}{2} $ 时,$ v = \frac{600}{t} = 600 \div \frac{15}{2} = 80 $,$\therefore $ 客车行驶速度 $ v $ 的取值范围为 $ 80 \mathrm{km/h} \leq v \leq 90 \mathrm{km/h} $。②不能。理由如下:$ 12 $ 时 $ 30 $ 分 $ - 8 $ 时 $ = \frac{9}{2}(\mathrm{h}) $,当 $ t = \frac{9}{2} $ 时,$ v = \frac{600}{t} = 600 \div \frac{9}{2} \approx 133 $。$\because 133 > 120 $,$\therefore $ 客车不能在当天 $ 12 $ 时 $ 30 $ 分前到达乙地。
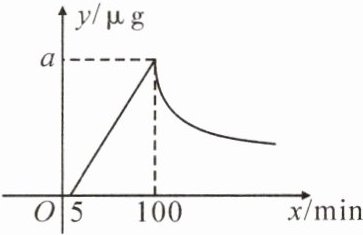
10. (常德澧县期中)某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第 5 min 起每分钟每毫升血液中的含药量增加 $ 0.2 \mu g $,第 100 min 达到最高,接着开始衰退.血液中的含药量 $ y ( \mu g ) $与时间 $ x ( min ) $的函数关系如图所示,并发现衰退时 y 与 x 成反比例函数关系.
(1)a 的值为______;
(2)当 $ x > 100 $时,y 与 x 之间的函数表达式为______;
(3)如果每毫升血液中的含药量不低于 $ 10 \mu g $时是有效的,求一次服药后的有效时间有多久.
(1)a 的值为______;
(2)当 $ x > 100 $时,y 与 x 之间的函数表达式为______;
(3)如果每毫升血液中的含药量不低于 $ 10 \mu g $时是有效的,求一次服药后的有效时间有多久.

答案:
解:
(1) $ 19 $
(2) $ y = \frac{1900}{x} $
(3)当 $ 5 \leq x \leq 100 $ 时,$ y $ 与 $ x $ 的函数表达式为 $ y = 0.2x - 1 $,当 $ y = 10 $ 时,$ 0.2x - 1 = 10 $,解得 $ x = 55 $。在 $ y = \frac{1900}{x} $ 中,当 $ y = 10 $ 时,$ \frac{1900}{x} = 10 $,解得 $ x = 190 $,$\therefore 190 - 55 = 135(\mathrm{min}) $,$\therefore $ 一次服药后的有效时间有 $ 135 \mathrm{min} $。
(1) $ 19 $
(2) $ y = \frac{1900}{x} $
(3)当 $ 5 \leq x \leq 100 $ 时,$ y $ 与 $ x $ 的函数表达式为 $ y = 0.2x - 1 $,当 $ y = 10 $ 时,$ 0.2x - 1 = 10 $,解得 $ x = 55 $。在 $ y = \frac{1900}{x} $ 中,当 $ y = 10 $ 时,$ \frac{1900}{x} = 10 $,解得 $ x = 190 $,$\therefore 190 - 55 = 135(\mathrm{min}) $,$\therefore $ 一次服药后的有效时间有 $ 135 \mathrm{min} $。
查看更多完整答案,请扫码查看


