《2025年课时夺冠九年级数学上册湘教版》

10. 已知关于 $x$ 的方程 $x^2 - 2x + m = 0$ 有两个相等的实数根,则 $m$ 的值为()
A. $3$
B. $2$
C. $1$
D. $0$

答案： C

11. (永州冷水滩区期中)已知 $x_1,x_2$ 是方程 $x^2 - 4x + 1 = 0$ 的两个根,则 $(x_1 + 1)(x_2 + 1)$ 的值为()
A. $-2$
B. $4$
C. $6$
D. $-4$

答案： C

12. 对于实数 $a,b$ 定义运算“☆”如下:$a☆b = ab^2 - ab$,例如,$3☆2 = 3×2^2 - 3×2 = 6$,则方程 $1☆x = 2$ 的根的情况为()
A. 没有实数根
B. 只有一个实数根
C. 有两个相等的实数根
D. 有两个不相等的实数根

答案： D

13. 已知 $x_1,x_2$ 是关于 $x$ 的一元二次方程 $x^2 - (2m + 3)x + m^2 = 0$ 的两个不相等的实数根,且满足 $\frac{1}{x_1} + \frac{1}{x_2} = 1$,则 $m$ 的值为______.

答案： 3

14. 已知 $a,b$ 是方程 $x^2 + x - 3 = 0$ 的两个实数根,则 $a^2 - b + 2024$ 的值是______.

答案： 2 028

15. 已知关于 $x$ 的一元二次方程 $x^2 - 2x - 3m^2 = 0$.
(1)求证:无论 $m$ 取何值,方程总有两个不相等的实数根;
(2)若方程的两个实数根分别为 $\alpha,\beta$,且 $\alpha + 2\beta = 5$,求 $m$ 的值.

答案：
(1) 证明: 由题意, 得$\Delta = (-2)^2 - 4\times1\times(-3m^2) = 4 + 12m^2 ＞ 0$,$\therefore$无论$m$取何值, 方程总有两个不相等的实数根.
(2) 解: 由根与系数的关系, 得$\alpha + \beta = 2$,$\alpha\beta = -3m^2$.$\because\alpha + 2\beta = 5$,$\therefore\alpha + \beta + \beta = 5$,$\therefore 2 + \beta = 5$,$\therefore\beta = 3$,$\therefore\alpha = -1$,$\therefore -3m^2 = \alpha\beta = -3$, 解得$m = \pm1$.

16. (株洲炎陵县期末)已知关于 $x$ 的一元二次方程 $x^2 + 2mx + m^2 + m = 0$ 有两个不相等的实数根.
(1)求 $m$ 的取值范围;
(2)设 $x_1,x_2$ 是方程的两个根,且 $x_1^2 + x_2^2 = 12$,求 $m$ 的值.

答案： 解:
(1) 由题意, 得$\Delta = (2m)^2 - 4(m^2 + m) ＞ 0$, 解得$m ＜ 0$.
(2) 由根与系数的关系, 得$x_1 + x_2 = -2m$,$x_1x_2 = m^2 + m$.$\because x_1^2 + x_2^2 = 12$,$\therefore (x_1 + x_2)^2 - 2x_1x_2 = 12$, 即$(-2m)^2 - 2(m^2 + m) = 12$, 解得$m_1 = -2$,$m_2 = 3$. 由
(1) 知$m ＜ 0$,$\therefore m = -2$.

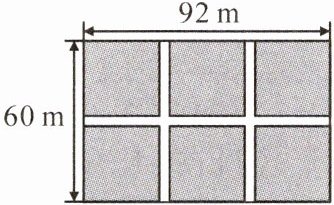
17. (衡阳石鼓区月考)如图,在一块长 $92m$、宽 $60m$ 的矩形耕地上挖三条水渠(水渠的宽都相等),水渠把耕地分成 $6$ 个矩形小块(阴影部分).如果 $6$ 个矩形小块的面积和为 $5310m^2$,那么水渠应挖多宽? 若设水渠应挖 $x m$ 宽,则下面所列方程中正确的是()

A. $(92 - 2x)(60 - x) = 5310$
B. $92×60 - 2×60x - 92x - 2x^2 = 5310$
C. $92×60 - 2×60x - 92x = 5310$
D. $92×60 - 2×92x - 60x + 2x^2 = 5310$

答案： A

18. (怀化溆浦县月考)某校九年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛 $45$ 场,则参加此次比赛的球队数是()
A. $8$
B. $9$
C. $10$
D. $11$

答案： C

19. 一个两位数等于其各数位上数字的积的 $3$ 倍,且个位上的数字比十位上的数字大 $2$,则这个两位数是______.

答案： 24