第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
7. 将一块矩形桌布铺在长为3m、宽为2m的矩形桌面上,各边下垂的长度相同,并且桌布的面积是桌面面积的2倍,那么桌布下垂的长度为()
A. 1.5m
B. 2.5m
C. 0.5m
D. 1m
A. 1.5m
B. 2.5m
C. 0.5m
D. 1m
答案:
C
8. 如图,在一块长22m,宽为14m的矩形空地内修建三条
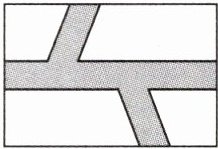
宽度相等的小路,其余部分种植花草.若花草的种植面积为$240m^2,$则小路的宽为______m.

宽度相等的小路,其余部分种植花草.若花草的种植面积为$240m^2,$则小路的宽为______m.
答案:
2
9. 如图,某小区矩形绿地的长、宽分别为35m,15m.现计划对其进行扩建,将绿地的长、宽增加相同的长度后,得到一块新的矩形绿地.
(1)若扩建后的矩形绿地面积为$800m^2,$求新的矩形绿地的长与宽;
(2)扩建后,实地测量发现新的矩形绿地的长是宽的5/3倍.求新的矩形绿地的面积.
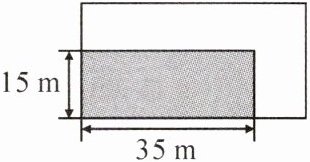
(1)若扩建后的矩形绿地面积为$800m^2,$求新的矩形绿地的长与宽;
(2)扩建后,实地测量发现新的矩形绿地的长是宽的5/3倍.求新的矩形绿地的面积.

答案:
解:(1)设绿地的长、宽都增加 $ x $ m,则新的矩形绿地的长为 $ (35 + x) $ m,宽为 $ (15 + x) $ m. 根据题意,得 $ (35 + x)(15 + x) = 800 $,解得 $ x_{1} = 5 $,$ x_{2} = -55 $(不合题意,舍去),$ \therefore 35 + x = 35 + 5 = 40 $,$ 15 + x = 15 + 5 = 20 $. 答:新的矩形绿地的长为 40 m,宽为 20 m. (2)设绿地的长、宽都增加 $ y $ m,则新的矩形绿地的长为 $ (35 + y) $ m,宽为 $ (15 + y) $ m. 根据题意,得 $ \frac{35 + y}{15 + y} = \frac{5}{3} $,解得 $ y = 15 $,$ \therefore (35 + y)(15 + y) = (35 + 15) \times (15 + 15) = 1500 $. 答:新的矩形绿地的面积为 $ 1500 $ $ m^{2} $.
10. 如图,要利用一面足够长的墙为一边,其余三边用总长33m的围栏建两个面积相等的生态园.为了出入方便,每个生态园在平行于墙的一边各留了一个宽1.5m的门,能够建生态园的场地垂直于墙的一边的长不超过6m(围栏宽忽略不计).
(1)若每个生态园的面积为$48m^2,$求每个生态园平行于墙的一边的长;
(2)每个生态园的面积______(填“能”或“不能”)达到$108m^2.$
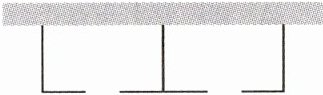
(1)若每个生态园的面积为$48m^2,$求每个生态园平行于墙的一边的长;
(2)每个生态园的面积______(填“能”或“不能”)达到$108m^2.$

答案:
解:(1)设每个生态园垂直于墙的一边长为 $ x $ m. 根据题意,得 $ x(33 + 1.5 \times 2 - 3x) = 48 \times 2 $,解得 $ x_{1} = 4 $,$ x_{2} = 8 $(不合题意,舍去),$ \therefore 33 + 1.5 \times 2 - 3x = 24 $,$ 24 \div 2 = 12 $. 答:每个生态园平行于墙的一边的长为 12 m. (2)不能
11. (益阳资阳区期末)如图,在矩形ABCD中,AB= 6cm,BC= 12cm,点P从点A出发沿AB以1cm/s的速度向点B运动,同时,点Q从点B出发沿BC以2cm/s的速度向点C运动.设运动时间为x s.
(1)若PQ= 4√2cm,求x的值;
(2)若△DPQ的面积为$31cm^2,$求x的值.
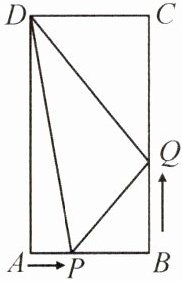
(1)若PQ= 4√2cm,求x的值;
(2)若△DPQ的面积为$31cm^2,$求x的值.

答案:
解:由题意,得 $ AP = x $ cm,$ BQ = 2x $ cm,$ \therefore BP = AB - AP = (6 - x) $ cm,$ CQ = BC - BQ = (12 - 2x) $ cm. (1)$ \because $ 四边形 $ ABCD $ 是矩形,$ \therefore \angle B = 90^{\circ} $,$ \therefore BP^{2} + BQ^{2} = PQ^{2} $,即 $ (6 - x)^{2} + (2x)^{2} = (4\sqrt{2})^{2} $,解得 $ x_{1} = \frac{2}{5} $,$ x_{2} = 2 $,$ \therefore x $ 的值为 $ \frac{2}{5} $ 或 2. (2)$ \because $ 四边形 $ ABCD $ 是矩形,$ \therefore CD = AB = 6 $ cm,$ AD = BC = 12 $ cm,$ \angle A = \angle B = \angle C = 90^{\circ} $. $ \because S_{\triangle DPQ} = S_{矩形ABCD} - S_{\triangle ADP} - S_{\triangle CDQ} - S_{\triangle BPQ} $,$ \therefore AB \cdot BC - \frac{1}{2}AD \cdot AP - \frac{1}{2}CD \cdot CQ - \frac{1}{2}BP \cdot BQ = 31 $,即 $ 6 \times 12 - \frac{1}{2} \times 12x - \frac{1}{2} \times 6(12 - 2x) - \frac{1}{2}(6 - x) \cdot 2x = 31 $,解得 $ x_{1} = 1 $,$ x_{2} = 5 $,$ \therefore x $ 的值为 1 或 5.
查看更多完整答案,请扫码查看


