《2025年课时夺冠九年级数学上册湘教版》

11. 点 $ M(-\sin 60^{\circ}, \sin 30^{\circ}) $ 关于 $ x $ 轴对称的点的坐标是()
A. $ (\frac{\sqrt{3}}{2}, \frac{1}{2}) $
B. $ (-\frac{\sqrt{3}}{2}, -\frac{1}{2}) $
C. $ (-\frac{\sqrt{3}}{2}, \frac{1}{2}) $
D. $ (-\frac{1}{2}, -\frac{\sqrt{3}}{2}) $

答案： B

12. 已知 $ \angle A $ 为锐角,下列结论：① $ \sin A ＞ 0 $；②若 $ 45^{\circ} ＜ \angle A ＜ 60^{\circ} $,则 $ \frac{\sqrt{2}}{2} ＜ \sin A ＜ \frac{\sqrt{3}}{2} $；③ $ \sqrt{(1 - \sin A)^{2}} = 1 - \sin A $。其中正确的有()
A. $ 0 $ 个
B. $ 1 $ 个
C. $ 2 $ 个
D. $ 3 $ 个

答案： D

13. 在 $ \text{Rt}\triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AB = 2 $,$ BC = \sqrt{3} $,则 $ \sin \frac{A}{2} $ 的值为______。

答案： $\frac{1}{2}$

14. 计算：
(1) $ \sqrt{(\frac{1}{2} - \sin 45^{\circ})^{2}} - |2\sin 60^{\circ} - \sin 30^{\circ}| $；
(2) $ \frac{1}{2}\sin 60^{\circ} + \frac{\sqrt{2}}{2}\sin 45^{\circ} + \sin 30^{\circ} $。

答案： 解：
(1) 原式 $=\sqrt{\left(\frac{1}{2}-\frac{\sqrt{2}}{2}\right)^{2}}-\left|2 \times \frac{\sqrt{3}}{2}-\frac{1}{2}\right|=\frac{\sqrt{2}}{2}-\frac{1}{2}-\sqrt{3}+\frac{1}{2}=\frac{\sqrt{2}}{2}-\sqrt{3}$。
(2) 原式 $=\frac{1}{2} \times \frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2} \times \frac{\sqrt{2}}{2}+\frac{1}{2}=\frac{\sqrt{3}}{4}+\frac{1}{2}+\frac{1}{2}=\frac{\sqrt{3}}{4}+1$。

15. 已知锐角 $ \alpha $,关于 $ x $ 的一元二次方程 $ x^{2} - 2x\sin \alpha + \sqrt{3}\sin \alpha - \frac{3}{4} = 0 $ 有两个相等的实数根,求 $ \alpha $ 的度数。

答案： 解：由题意，得 $\Delta=(2 \sin \alpha)^{2}-4\left(\sqrt{3} \sin \alpha-\frac{3}{4}\right)=0$，解得 $\sin \alpha=\frac{\sqrt{3}}{2}$，$\therefore \alpha=60^{\circ}$。

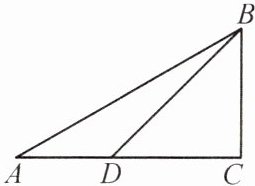
16. 如图,在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,点 $ D $ 在 $ AC $ 上,已知 $ \angle BDC = 45^{\circ} $,$ BD = 10\sqrt{2} $,$ AB = 20 $。求 $ \angle A $ 的度数。

答案： 解：在 $\mathrm{Rt} \triangle B C D$ 中，$\because \sin \angle B D C=\frac{B C}{B D}$，$\therefore B C=B D \cdot \sin \angle B D C=10 \sqrt{2} \times \sin 45^{\circ}=10$，$\therefore$ 在 $\mathrm{Rt} \triangle A B C$ 中，$\sin A=\frac{B C}{A B}=\frac{10}{20}=\frac{1}{2}$，$\therefore \angle A=30^{\circ}$。

17. (株洲渌口区期末)(1)用计算器计算并验证 $ \sin 25^{\circ} + \sin 46^{\circ} $ 与 $ \sin 71^{\circ} $ 之间的大小关系；
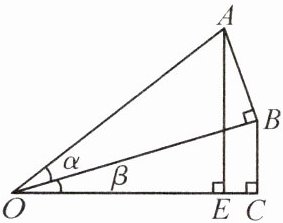
(2)若 $ \alpha $,$ \beta $,$ \alpha + \beta $ 都是锐角,猜想 $ \sin \alpha + \sin \beta $ 与 $ \sin (\alpha + \beta) $ 之间的大小关系；
(3)请借助如图所示的图形证明上述猜想。

答案：
(1) 解：$\because \sin 25^{\circ}+\sin 46^{\circ} \approx 0.423+0.719=1.142$，$\sin 71^{\circ} \approx 0.945$，$\therefore \sin 25^{\circ}+\sin 46^{\circ}＞\sin 71^{\circ}$。
(2) 解：$\sin \alpha+\sin \beta＞\sin (\alpha+\beta)$。
(3) 证明：$\because \sin \alpha+\sin \beta=\frac{A B}{O A}+\frac{B C}{O B}$，$\sin (\alpha+\beta)=\frac{A E}{O A}$，且 $O A＞O B$，$\therefore \frac{B C}{O B}＞\frac{B C}{O A}$，$\therefore \frac{A B}{O A}+\frac{B C}{O B}＞\frac{A B}{O A}+\frac{B C}{O A}=\frac{A B+B C}{O A}$。$\because A B+B C＞A E$，$\therefore \frac{A B+B C}{O A}＞\frac{A E}{O A}$，$\therefore \sin \alpha+\sin \beta＞\sin (\alpha+\beta)$。