《2025年课时夺冠九年级数学上册湘教版》

10. 如图,在$Rt\triangle ABC$中,CD是斜边AB上的高,则图中的相似三角形共有()

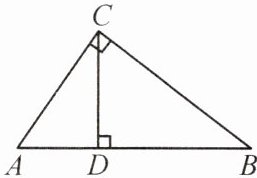
A. 1对
B. 2对
C. 3对
D. 4对

答案： C

11.(湘潭雨湖区期中)如图,一束光线从y轴上的点$A(0,1)$发出,经过x轴上点C反射后,经过点$B(6,2)$,则点C的坐标是______.

答案： $ ( 2,0 ) $

12. 如图,在矩形ABCD中,$AB = 3$,$BC = 10$,点E在BC边上,$DF⊥AE$,交AE的延长线于点F. 若$DF = 6$,则线段EF的长为______.

答案： 3

13. 如图,在$\triangle ABC$中,$∠BAC = 90^{\circ}$,M是BC的中点,过点A作AM的垂线,交CB的延长线于点D. 求证：$\triangle DBA \backsim \triangle DAC$.

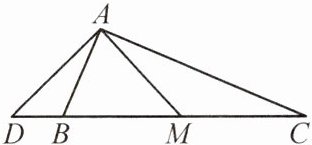
答案： 证明：
∵ $ \angle BAC = 90 ^ { \circ } $，$ M $ 是 $ BC $ 的中点，
∴ $ AM = CM $，
∴ $ \angle C = \angle CAM $．
∵ $ DA \perp AM $，
∴ $ \angle DAM = 90 ^ { \circ } = \angle BAC $，
∴ $ \angle DAB + \angle BAM = \angle CAM + \angle BAM = 90 ^ { \circ } $，
∴ $ \angle DAB = \angle CAM $，
∴ $ \angle DAB = \angle C $．
∵ $ \angle D = \angle D $，
∴ $ \triangle DBA \backsim \triangle DAC $．

14. 如图,在正方形ABCD中,M为BC上一点,F是AM的中点,$EF⊥AM$,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证：$\triangle ABM \backsim \triangle EFA$；

(2)若$AB = 12$,$BM = 5$,求DE的长.

答案：
(1) 证明：
∵ 四边形 $ ABCD $ 是正方形，
∴ $ \angle B = 90 ^ { \circ } $，$ AD // BC $，
∴ $ \angle AMB = \angle EAF $．
∵ $ EF \perp AM $，
∴ $ \angle AFE = 90 ^ { \circ } $，
∴ $ \angle B = \angle AFE $，
∴ $ \triangle ABM \backsim \triangle EFA $．
(2) 解：由
(1) 知 $ \angle B = 90 ^ { \circ } $，
∴ $ AM = \sqrt { AB ^ { 2 } + BM ^ { 2 } } = \sqrt { 12 ^ { 2 } + 5 ^ { 2 } } = 13 $．
∵ $ F $ 是 $ AM $ 的中点，
∴ $ FA = \frac { 1 } { 2 } AM = 6.5 $．由
(1) 知 $ \triangle ABM \backsim \triangle EFA $，
∴ $ \frac { BM } { FA } = \frac { AM } { EA } $，即 $ \frac { 5 } { 6.5 } = \frac { 13 } { EA } $，解得 $ EA = 16.9 $．
∵ 四边形 $ ABCD $ 是正方形，
∴ $ AD = AB = 12 $，
∴ $ DE = EA - AD = 4.9 $．

15.(常德汉寿县月考)如图,$\triangle ABC和\triangle DEP$是两个全等的等腰直角三角形,$∠BAC = ∠PDE = 90^{\circ}$.
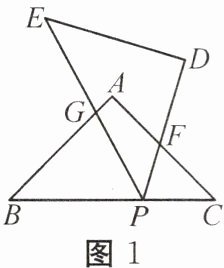
(1)若$\triangle DEP$的顶点P在BC上(如图1),PD,PE分别与AC,AB相交于点F,G. 求证：$\triangle PBG \backsim \triangle FCP$；
(2)若使$\triangle DEP$的顶点P与$\triangle ABC$的顶点A重合(如图2),PD,PE分别与BC相交于点F,G. 试问$\triangle PBG与\triangle FCP$还相似吗？为什么？

答案：
(1) 证明：
∵ $ \triangle ABC $ 和 $ \triangle DEP $ 是两个全等的等腰直角三角形，
∴ $ \angle B = \angle C = \angle DPE $．
∵ $ \angle B + \angle BGP = \angle DPE + \angle CPF $，
∴ $ \angle BGP = \angle CPF $，
∴ $ \triangle PBG \backsim \triangle FCP $．
(2) 解：$ \triangle PBG $ 与 $ \triangle FCP $ 相似．理由如下：
∵ $ \triangle ABC $ 和 $ \triangle DEP $ 是两个全等的等腰直角三角形，
∴ $ \angle B = \angle C = \angle DPE = 45 ^ { \circ } $．
∵ $ \angle BGP = \angle C + \angle CPG = 45 ^ { \circ } + \angle CAG $，$ \angle CPF = \angle DPE + \angle CAG = 45 ^ { \circ } + \angle CAG $，
∴ $ \angle BGP = \angle CPF $，
∴ $ \triangle PBG \backsim \triangle FCP $．