《2025年课时夺冠九年级数学上册湘教版》

11. 有下列关于$ x $的方程:①$ a x ^ { 2 } + b x + c = 0 $;②$ 3 x ( x - 4 ) = 0 $;③$ x ^ { 2 } + y - 3 = 0 $;④$ \frac { 1 } { 2 } + x = 2 $;⑤$ x ^ { 3 } - 3 x + 8 = 0 $;⑥$ \frac { 1 } { 2 } x ^ { 2 } - 5 x + 7 = 0 $;⑦$ ( x - 2 ) ( x + 5 ) = x ^ { 2 } - 1 $.其中一定是一元二次方程的有()
A. $ 2 $个
B. $ 3 $个
C. $ 4 $个
D. $ 5 $个

答案： A

12. 若关于$ x 的一元二次方程 ( m - 2 ) x ^ { 2 } + m ^ { 2 } x = 4 x + 5 $化为一般形式后不含一次项,则$ m $的值为()
A. $ 0 $
B. $ \pm 2 $
C. $ 2 $
D. $ - 2 $

答案： D

13. 已知关于$ x 的方程 ( a - 2 ) x ^ { 2 } + \sqrt { a - 1 } x + 1 = 0 $是一元二次方程,那么$ a $的取值范围是____.

答案： $ a \geq 1 $ 且 $ a \neq 2 $

14. (长沙期末)端午节期间,某食品专卖店准备了一批粽子,每盒利润为$ 50 $元,平均每天可卖$ 300 $盒,经过调查发现每降价$ 1 $元,可多销售$ 10 $盒.为了尽快减少库存,决定采取降价措施,专卖店要想平均每天盈利$ 16000 $元,设每盒粽子降价$ x $元,则可列方程为____,化成一般形式为____.

答案： $ ( 50 - x ) ( 300 + 10 x ) = 16000 $ $ x ^ { 2 } - 20 x + 100 = 0 $

15. 已知关于$ x 的方程 ( m + 3 ) ( m - 3 ) x ^ { 2 } + ( m + 3 ) x + 2 = 0 $.
(1)当$ m $为何值时,此方程是一元一次方程?
(2)当$ m $为何值时,此方程是一元二次方程?

答案： 解：
(1)由题意，得 $ ( m + 3 ) ( m - 3 ) = 0 $ 且 $ m + 3 \neq 0 $，$ \therefore m - 3 = 0 $，即 $ m = 3 $。
(2)由题意，得 $ ( m + 3 ) ( m - 3 ) \neq 0 $，即 $ m \neq \pm 3 $。

16. 根据下列问题列方程,并将所列方程化成一元二次方程的一般形式.
(1)参加足球联赛的每两支球队之间都要进行一场比赛,共要比赛$ 55 $场,求参加比赛的球队的数量;
(2)某小组每两名同学之间互赠一件礼物,全组共赠送礼物$ 182 $件,求全组的人数;
(3)如图,用$ 100 \mathrm { m } 长的围栏围成总面积为 400 \mathrm { m } ^ { 2 } $的三个大小相同的矩形羊圈,羊圈的一面靠墙(墙足够长),求$ AB $的长.

答案： 解：
(1)设参加比赛的球队的数量为 $ x $。由题意，得 $ \frac { 1 } { 2 } x ( x - 1 ) = 55 $，化成一般形式，得 $ x ^ { 2 } - x - 110 = 0 $。
(2)设全组有 $ x $ 人。由题意，得 $ x ( x - 1 ) = 182 $，化成一般形式，得 $ x ^ { 2 } - x - 182 = 0 $。
(3)设 $ AB $ 的长为 $ x $ m。由题意，得 $ x ( 100 - 4 x ) = 400 $，化成一般形式，得 $ x ^ { 2 } - 25 x + 100 = 0 $。

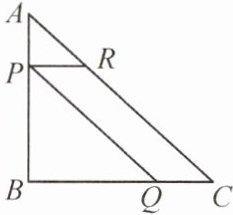
17. (怀化期中)如图,在等腰直角三角形$ A B C $中,$ \angle B = 90 ^ { \circ } $,$ A B = B C = 8 \mathrm { cm } $.动点$ P 从点 A 出发沿 A B 向点 B $移动,过点$ P 作 P Q // A C $,$ P R // B C $.当$ A P $的长为多少时,$ //ogram P Q C R 的面积为 16 \mathrm { cm } ^ { 2 } $? 设$ A P 的长为 x \mathrm { cm } $,列出关于$ x $的方程,并化成一般形式.

答案： 解：由题意，易得 $ \triangle A P R $ 为等腰直角三角形，$ \therefore P R = A P = x $ cm，$ \therefore B P = A B - A P = ( 8 - x ) $ cm。$ \because \square P Q C R $ 的面积为 $ 16 $ $ cm ^ { 2 } $，$ \therefore P R \cdot B P = 16 $ $ cm ^ { 2 } $，即 $ x ( 8 - x ) = 16 $，化成一般形式为 $ x ^ { 2 } - 8 x + 16 = 0 $。