第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
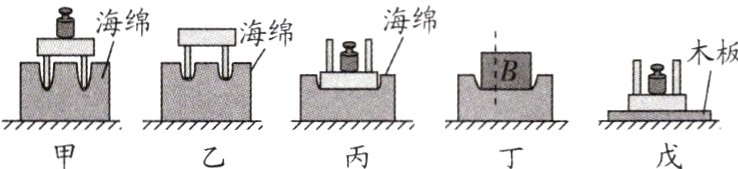
16.(2024·南京鼓楼区期末)小明利用如图所示的器材探究影响压力作用效果的因素.
(1)该实验是通过观察______来显示压力的作用效果.
(2)比较甲、丙两图,可得到结论:______.
(3)小明将物体B沿竖直方向切成大小不同的两块,如图丁所示,他发现它们对海绵的压力作用效果相同,由此他得出结论:压力作用效果与受力面积无关. 他在探究过程中存在的问题是______.
(4)若将小桌和砝码放在如图戊所示的木板上,则图戊中木板受到的压强$p_{戊}$和图丙中海绵受到的压强$p_{丙}$的大小关系为$p_{戊}$______(填“>”“<”或“=”)$p_{丙}$.
(1)该实验是通过观察______来显示压力的作用效果.
(2)比较甲、丙两图,可得到结论:______.
(3)小明将物体B沿竖直方向切成大小不同的两块,如图丁所示,他发现它们对海绵的压力作用效果相同,由此他得出结论:压力作用效果与受力面积无关. 他在探究过程中存在的问题是______.
(4)若将小桌和砝码放在如图戊所示的木板上,则图戊中木板受到的压强$p_{戊}$和图丙中海绵受到的压强$p_{丙}$的大小关系为$p_{戊}$______(填“>”“<”或“=”)$p_{丙}$.

答案:
(1)海绵的形变程度
(2)压力一定时,受力面积越小,压力的作用效果越明显
(3)没有控制压力大小相同
(4)=
(1)海绵的形变程度
(2)压力一定时,受力面积越小,压力的作用效果越明显
(3)没有控制压力大小相同
(4)=
17. 核心素养科学探究 如图1所示的三个高度相同的实心铁块放在水平桌面上,已知正方体铁块A最重,圆柱体铁块C的底面积最小. 哪个铁块对桌面的压强最大呢?同学们提出了以下三种猜想:
猜想一:正方体铁块A最重,所以它对桌面的压强最大.
猜想二:圆柱体铁块C的底面积最小,所以它对桌面的压强最大.
猜想三:三铁块的高度相同,所以它们对桌面的压强相等.
(1)以图1中长方体铁块B为研究对象,推导它对桌面的压强大小的表达式(已知铁的密度为$\rho$,长方体铁块的高度为h,底面积为S):p = ______(写出推导过程). 由上面压强的表达式可知,铁块对桌面的压强只与______有关,所以猜想______是正确的.
(2)利用海绵或其他简易器材,设计一个实验粗略验证上面的猜想:______.
(3)如图2中甲所示,密度均匀的柱体物块静止在水平面上时,它对水平面的压强为p. 若沿竖直方向切成如图2中乙所示的两部分,它们对水平面的压强分别为$p_{a}$和$p_{b}$,则p、$p_{a}$、$p_{b}$三者的大小关系为______;若将它沿斜线方向切成如图2中丙所示的两部分,它们对水平面的压强分别为$p_{c}$和$p_{d}$,则p、$p_{c}$、$p_{d}$三者的关系为______. 计算结果说明:第(1)问中推导出的压强表达式,适用于密度均匀的______(填“柱体”或“柱体及非柱体”).
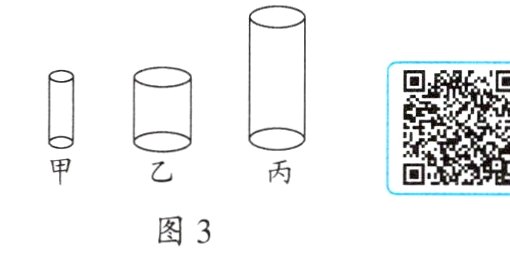
(4)如图3所示,有三个实心圆柱体甲、乙、丙,放在水平地面上,其中甲、乙高度相同,乙、丙的底面积相同,三者对地面的压强相等. 利用上述推导结论,请你判断以下选项中正确的是______.
A. $\rho_{甲}=\rho_{乙}>\rho_{丙}$
B. $\rho_{甲}=\rho_{乙}=\rho_{丙}$
C. $m_{甲}=m_{乙}=m_{丙}$
D. $m_{甲}>m_{乙}=m_{丙}$


猜想一:正方体铁块A最重,所以它对桌面的压强最大.
猜想二:圆柱体铁块C的底面积最小,所以它对桌面的压强最大.
猜想三:三铁块的高度相同,所以它们对桌面的压强相等.
(1)以图1中长方体铁块B为研究对象,推导它对桌面的压强大小的表达式(已知铁的密度为$\rho$,长方体铁块的高度为h,底面积为S):p = ______(写出推导过程). 由上面压强的表达式可知,铁块对桌面的压强只与______有关,所以猜想______是正确的.
(2)利用海绵或其他简易器材,设计一个实验粗略验证上面的猜想:______.
(3)如图2中甲所示,密度均匀的柱体物块静止在水平面上时,它对水平面的压强为p. 若沿竖直方向切成如图2中乙所示的两部分,它们对水平面的压强分别为$p_{a}$和$p_{b}$,则p、$p_{a}$、$p_{b}$三者的大小关系为______;若将它沿斜线方向切成如图2中丙所示的两部分,它们对水平面的压强分别为$p_{c}$和$p_{d}$,则p、$p_{c}$、$p_{d}$三者的关系为______. 计算结果说明:第(1)问中推导出的压强表达式,适用于密度均匀的______(填“柱体”或“柱体及非柱体”).
(4)如图3所示,有三个实心圆柱体甲、乙、丙,放在水平地面上,其中甲、乙高度相同,乙、丙的底面积相同,三者对地面的压强相等. 利用上述推导结论,请你判断以下选项中正确的是______.
A. $\rho_{甲}=\rho_{乙}>\rho_{丙}$
B. $\rho_{甲}=\rho_{乙}=\rho_{丙}$
C. $m_{甲}=m_{乙}=m_{丙}$
D. $m_{甲}>m_{乙}=m_{丙}$



答案:
(1) $\frac{F}{S}=\frac{G}{S}=\frac{mg}{S}=\frac{\rho Vg}{S}=\frac{\rho Shg}{S}=\rho gh$ 铁块的高度和密度
三
(2)将三个铁块竖直放置在海绵上,观察比较海绵的凹陷的深度,若深度相同,则可验证猜想三正确
(3) $p = p_{a}=p_{b}$ $p_{d}>p>p_{c}$ 柱体
(4)A
解析:本题涉及的知识是压强公式的应用(利用理论推导来验证猜想)和实验方案的设计.
(1)铁块 $B$ 对桌面的压强由重力产生:$F = G = mg$,$m = \rho V$,$V = Sh$,$p=\frac{F}{S}=\frac{G}{S}=\frac{mg}{S}=\frac{\rho Vg}{S}=\frac{\rho Shg}{S}=\rho gh$,即 $p = \rho gh$. 铁块对桌面的压强只与铁块的高度和密度有关,所以猜想三是正确的.
(2)为粗略验证猜想三,可以通过海绵的凹陷程度来粗略显示压强的大小.
(3)原来的柱体放在水平地面上,对地面的压强为 $p=\frac{G}{S}=\frac{\rho Vg}{S}=\frac{\rho Shg}{S}=\rho gh$,若将它沿竖直方向切成如题图 2 中乙所示的两部分,它们对水平面的压强:$p_{a}=p_{b}=p=\rho gh$;若沿如题图 2 中丙所示的方向切成 $c、d$ 两部分,由题图 2 中丙可知:$V_{c}<S_{c}h$,$p_{c}=\frac{G_{c}}{S_{c}}=\frac{\rho V_{c}g}{S_{c}}<\frac{\rho S_{c}hg}{S_{c}}=\rho gh = p$,$V_{d}>S_{d}h$,$p_{d}=\frac{G_{d}}{S_{d}}=\frac{\rho V_{d}g}{S_{d}}>\frac{\rho S_{d}hg}{S_{d}}=\rho gh = p$,由以上可知:$p_{d}>p>p_{c}$. 该计算结果说明,第
(1)问中推导出的压强表达式,只适用于密度均匀的柱体,对非柱体不成立.
(4)由题图 3 知甲、乙、丙的高度 $h_{甲}=h_{乙}<h_{丙}$,且三者对地面的压强相等,所以由 $p = \rho gh$ 可知,三圆柱体的密度关系为 $\rho_{甲}=\rho_{乙}>\rho_{丙}$;由题图 3 知甲、乙的底面积 $S_{甲}<S_{乙}$,高度 $h_{甲}=h_{乙}$,所以 $V_{甲}<V_{乙}$,因为 $\rho_{甲}=\rho_{乙}$,$m = \rho V$,所以甲、乙圆柱体的质量关系为 $m_{甲}<m_{乙}$;已知乙、丙的底面积 $S_{乙}=S_{丙}$,对地面的压强相等,则由 $p=\frac{F}{S}=\frac{G}{S}=\frac{mg}{S}$ 可知,乙、丙圆柱体的质量关系为 $m_{乙}=m_{丙}$;所以三圆柱体的质量关系为 $m_{甲}<m_{乙}=m_{丙}$;故 A 正确、BCD 错误.
(1) $\frac{F}{S}=\frac{G}{S}=\frac{mg}{S}=\frac{\rho Vg}{S}=\frac{\rho Shg}{S}=\rho gh$ 铁块的高度和密度
三
(2)将三个铁块竖直放置在海绵上,观察比较海绵的凹陷的深度,若深度相同,则可验证猜想三正确
(3) $p = p_{a}=p_{b}$ $p_{d}>p>p_{c}$ 柱体
(4)A
解析:本题涉及的知识是压强公式的应用(利用理论推导来验证猜想)和实验方案的设计.
(1)铁块 $B$ 对桌面的压强由重力产生:$F = G = mg$,$m = \rho V$,$V = Sh$,$p=\frac{F}{S}=\frac{G}{S}=\frac{mg}{S}=\frac{\rho Vg}{S}=\frac{\rho Shg}{S}=\rho gh$,即 $p = \rho gh$. 铁块对桌面的压强只与铁块的高度和密度有关,所以猜想三是正确的.
(2)为粗略验证猜想三,可以通过海绵的凹陷程度来粗略显示压强的大小.
(3)原来的柱体放在水平地面上,对地面的压强为 $p=\frac{G}{S}=\frac{\rho Vg}{S}=\frac{\rho Shg}{S}=\rho gh$,若将它沿竖直方向切成如题图 2 中乙所示的两部分,它们对水平面的压强:$p_{a}=p_{b}=p=\rho gh$;若沿如题图 2 中丙所示的方向切成 $c、d$ 两部分,由题图 2 中丙可知:$V_{c}<S_{c}h$,$p_{c}=\frac{G_{c}}{S_{c}}=\frac{\rho V_{c}g}{S_{c}}<\frac{\rho S_{c}hg}{S_{c}}=\rho gh = p$,$V_{d}>S_{d}h$,$p_{d}=\frac{G_{d}}{S_{d}}=\frac{\rho V_{d}g}{S_{d}}>\frac{\rho S_{d}hg}{S_{d}}=\rho gh = p$,由以上可知:$p_{d}>p>p_{c}$. 该计算结果说明,第
(1)问中推导出的压强表达式,只适用于密度均匀的柱体,对非柱体不成立.
(4)由题图 3 知甲、乙、丙的高度 $h_{甲}=h_{乙}<h_{丙}$,且三者对地面的压强相等,所以由 $p = \rho gh$ 可知,三圆柱体的密度关系为 $\rho_{甲}=\rho_{乙}>\rho_{丙}$;由题图 3 知甲、乙的底面积 $S_{甲}<S_{乙}$,高度 $h_{甲}=h_{乙}$,所以 $V_{甲}<V_{乙}$,因为 $\rho_{甲}=\rho_{乙}$,$m = \rho V$,所以甲、乙圆柱体的质量关系为 $m_{甲}<m_{乙}$;已知乙、丙的底面积 $S_{乙}=S_{丙}$,对地面的压强相等,则由 $p=\frac{F}{S}=\frac{G}{S}=\frac{mg}{S}$ 可知,乙、丙圆柱体的质量关系为 $m_{乙}=m_{丙}$;所以三圆柱体的质量关系为 $m_{甲}<m_{乙}=m_{丙}$;故 A 正确、BCD 错误.
查看更多完整答案,请扫码查看


