《2025年学霸题中题八年级物理下册苏科版》

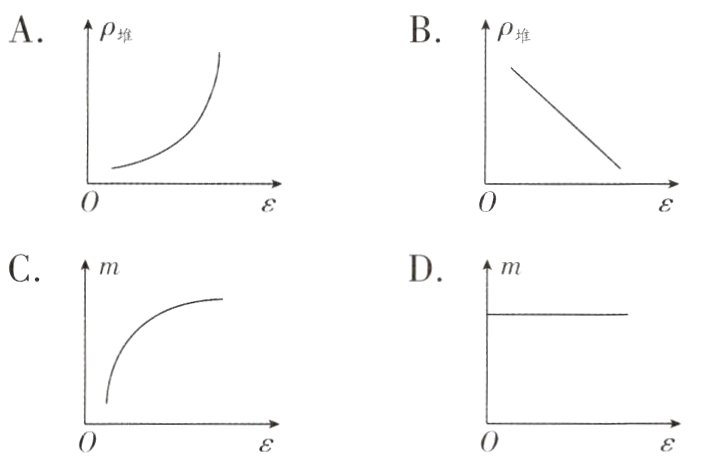
9. 核心素养 物理观念（2024·南通海门区期末）如图所示，固体颗粒放入容器中，颗粒间有孔隙.材料学上把孔隙体积与颗粒和孔隙总体积的比值称为孔隙率$\varepsilon$.将同种物质制成的大小不同的颗粒分别装满相同容器，下列描述堆密度${\rho }_{堆}$、颗粒和容器的总质量m与孔隙率$\varepsilon$的关系图线中，可能正确的是（ ）

答案： B 解析：CD. 根据题意，假设容器的体积为$V$，则颗粒的体积为$(1 - \varepsilon)V$，整体的质量等于颗粒的质量为$m=\rho_{颗}V_{颗}=\rho_{颗}V(1 - \varepsilon)$，可知，由于$\rho_{颗}$不变，颗粒和容器的总质量$m$与孔隙率$\varepsilon$的关系为一次函数，故CD错误；AB. 由公式可得，堆密度为$\rho_{堆}=\frac{m}{V}=\frac{\rho_{颗}V(1 - \varepsilon)}{V}=\rho_{颗}(1 - \varepsilon)$，可知，由于$\rho_{颗}$不变，则堆密度$\rho_{堆}$与孔隙率$\varepsilon$的关系为一次函数，且堆密度$\rho_{堆}$随着$\varepsilon$的增大而减小，故A错误，B正确。故选B。

10. 新素材 传统文化（2024·滨州中考）篆刻艺术是镌刻在中华艺术文脉上的古老印记.作为国粹之一，被联合国教科文组织列入《人类非物质文化遗产代表作名录》.如图所示，一位艺术家正在篆刻一枚方章，与篆刻前相比，篆刻后方章的质量________，密度________.（均填“变大”“变小”或“不变”）

答案： 变小 不变

11. 新素材 科技前沿（2024·扬州梅岭中学期中）科学家利用新技术研制出一种新型陶瓷材料，可用作火箭等高速飞行器的表面覆盖层，可见其具有很好的________（填“导热”或“隔热”）性；该材料即使在受到很大的空气阻力时变形也非常小，说明它具有很高的________（填“硬度”或“延展性”）；该陶瓷材料在常温下的密度为$2.7\times {10}^{3}kg/{m}^{3}$，从常温加热至900℃高温，体积收缩至原体积的90%，此时其密度为________$kg/{m}^{3}$.

答案： 隔热 硬度 $3\times10^3$

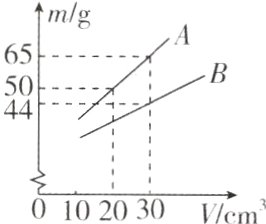
12. 甲、乙两个小球，它们的密度之比是3 : 2，质量之比是1 : 2，甲、乙两小球体积之比是________，如果甲切去一半，乙切去四分之一，剩下部分密度的比是________.一容器分别装入体积为V的A、B种液体后，液体和容器的总质量为M，M随V的变化关系如图中A和B所示，则容器的质量为________g，当容器装入40 cm³的A液体时，液体的质量为________g，A液体的密度为________$kg/{m}^{3}$，B液体的密度为________g/cm³.

答案： $1:3$ $3:2$ $20$ $60$ $1.5\times10^3$ $0.8$ 解析：由$\rho=\frac{m}{V}$可得$V=\frac{m}{\rho}$，则甲、乙两个小球的体积之比$V_{甲}:V_{乙}=\frac{m_{甲}}{\rho_{甲}}:\frac{m_{乙}}{\rho_{乙}}=\frac{m_{甲}}{m_{乙}}\times\frac{\rho_{乙}}{\rho_{甲}}=\frac{1}{2}\times\frac{2}{3}=1:3$；密度是物体的一种特性，其大小跟物体本身的体积和质量无关，剩余甲、乙小球的密度之比仍为$3:2$。由图像可知，当$A$的体积由$20\ cm^3$增加到$30\ cm^3$时，总质量增加了$\Delta m_A = 65\ g - 50\ g = 15\ g$，所以$A$液体的密度为$\rho_A=\frac{\Delta m_A}{\Delta V_A}=\frac{15\ g}{10\ cm^3}=1.5\ g/cm^3 = 1.5\times10^3\ kg/m^3$，当$A$液体为$20\ cm^3$时，其质量为$m_{A1}=\rho_A V_{A1}=1.5\ g/cm^3\times20\ cm^3 = 30\ g$，则容器的质量为$m_{容器}=m_1 - m_{A1}=50\ g - 30\ g = 20\ g$，$A$液体为$40\ cm^3$时的质量为$m_{A3}=\rho_A V_{A3}=1.5\ g/cm^3\times40\ cm^3 = 60\ g$。由图像可知，当$B$液体的体积为$30\ cm^3$时，液体和容器的质量为$44\ g$，此时$B$液体质量为$m_B = 44\ g - 20\ g = 24\ g$，$B$液体的密度为$\rho_B=\frac{m_B}{V_B}=\frac{24\ g}{30\ cm^3}=0.8\ g/cm^3$。

13. “玫瑰金”是一种黄金和铜的合金，由于颜色好看，深受年轻人的喜爱.现有一块玫瑰金，实验测出的质量为460 g，体积为40cm³，并从课本中查出了金、铜的密度分别是19.3 g/cm³和8.9 g/cm³.请根据实验结果计算这块玫瑰金的密度为________g/cm³，商店一般会用含金量（黄金的质量占合金质量的比值）来形容玫瑰金的品质，它的含金量为________%（结果保留一位小数）.

答案： $11.5$ $42.0$ 解析：由$\rho=\frac{m}{V}$可得，这块玫瑰金的密度为$\rho=\frac{m}{V}=\frac{460\ g}{40\ cm^3}=11.5\ g/cm^3$。设这块玫瑰金中黄金的质量为$m_1$，则铜的质量$m_2 = m_{总}-m_1 = 460\ g - m_1$，则合金的总体积为$V_{总}=V_1 + V_2=\frac{m_1}{\rho_{金}}+\frac{m_2}{\rho_{铜}}=\frac{m_1}{19.3\ g/cm^3}+\frac{460\ g - m_1}{8.9\ g/cm^3}=40\ cm^3$，解得$m_1 = 193\ g$，所以含金量为$\frac{m_1}{m_{总}}\times100\%=\frac{193\ g}{460\ g}\times100\%\approx42.0\%$。

14. (10分)(2024·南京联合体期末)小明测量物质的密度，进行了如下实验.

(1) 测量鹅卵石的密度.
①他将天平放在水平桌面上，将游码移至标尺的“0”刻度线处，并调节________，使指针指到分度盘中央刻度处.
②鹅卵石放在左盘内，当天平平衡时，右盘中砝码的质量及游码在标尺上的位置如图甲所示，测出了鹅卵石的质量m = ________g，然后他将鹅卵石放入盛有20 mL水的量筒中，液面位置如图乙所示.则鹅卵石的密度$\rho$ = ________$kg/{m}^{3}$.
(2) 小明利用上述密度为$\rho$的鹅卵石测量盐水的密度，设计了如下方案：
①在烧杯中放入适量的盐水将鹅卵石浸没，在液面到达的位置上作标记，用天平称出总质量为${m}_{1}$；
②将鹅卵石从盐水中取出，用天平称出剩余盐水和烧杯的总质量为${m}_{2}$；
③向烧杯中加盐水到标记处，再用天平称出此时盐水和烧杯的总质量为${m}_{3}$.
根据以上步骤可得出盐水密度的表达式为${\rho }_{盐水}$ = ________（用${m}_{1}$、${m}_{2}$、${m}_{3}$、$\rho$表示），此盐水密度测量值将________（填“偏大”“偏小”或“无影响”）.

答案：
(1)①平衡螺母 ②$62$ $3.1\times10^3$
(2)$\frac{m_3 - m_2}{m_1 - m_2}\rho$ 无影响
解析：
(1)①天平使用前要调节平衡，将天平放在水平桌面上，将游码移至标尺的“$0$”刻度线处，并调节平衡螺母，使指针指到分度盘中央刻度处。
②天平平衡时，左盘物体的质量等于右盘砝码的质量和游码示数的和，标尺的分度值为$0.2\ g$，游码在标尺上对应的刻度值$2\ g$，鹅卵石的质量即$m = 50\ g + 10\ g + 2\ g = 62\ g$，量筒的分度值为$2\ mL$，鹅卵石和水的总体积为$40\ mL$，得鹅卵石的体积为$V = 40\ mL - 20\ mL = 20\ mL = 20\ cm^3$，鹅卵石的密度为$\rho=\frac{m}{V}=\frac{62\ g}{20\ cm^3}=3.1\ g/cm^3 = 3.1\times10^3\ kg/m^3$。
(2)由题可知，实验使用的是上述实验中的鹅卵石，则步骤③中添加的盐水的质量为$m_{盐水}=m_3 - m_2$，添加的盐水的体积为$V_{盐水}=V_{石}=\frac{m_1 - m_2}{\rho}$，盐水的密度为$\rho_{盐水}=\frac{m_{盐水}}{V_{盐水}}=\frac{m_3 - m_2}{\frac{m_1 - m_2}{\rho}}=\frac{m_3 - m_2}{m_1 - m_2}\rho$。鹅卵石从盐水中取出时会带有部分盐水，但是将鹅卵石从盐水中取出后，再向烧杯中加盐水到标记处时，带出的水得到了补充，不影响增加的盐水的质量的测量，即此盐水密度测量值将无影响。