《2025年学霸题中题八年级物理下册苏科版》

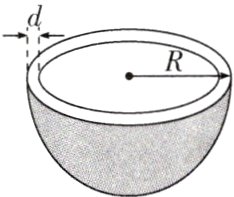
6. 在研究物体的沉浮条件时，一实验小组将一质量为54 g的橡皮泥放入盛水的水槽中，橡皮泥下沉. 老师请大家思考能否让橡皮泥漂浮在水面上呢? 他们经过思考后将橡皮泥捏成了如图所示的厚度均匀的半球状“小碗”，将碗口朝上轻轻放在水面上，小碗漂浮($\rho_{泥}=1.2 \text{g/cm}^{3}$, $\rho_{水}=1.0 \text{g/cm}^{3}$, 半球的体积公式是$V = \frac{2}{3} \pi R^{3}$, $\pi$取3，$\sqrt[3]{4.5}$取1.65，g取10 N/kg).
　(1) 求橡皮泥的体积.
　(2) 橡皮泥“小碗”漂浮在水面上受到的浮力是多少?
　(3) 橡皮泥“小碗”的厚度d要满足什么条件，才能够漂浮在水面上?
　　　　　　　　　　　　

答案： 6.
(1)4.5×10⁻⁵ m³
(2)0.54 N
(3)d ＜ 1.35 cm
解析：
(1)橡皮泥的质量m = 54 g，橡皮泥的密度为ρ_{泥} = 1.2 g/cm³，所以橡皮泥的体积为
V = $\frac{m}{\rho_{泥}}$ = $\frac{54 g}{1.2 g/cm^{3}}$ = 45 cm³ = 4.5×10⁻⁵ m³.
(2)根据物体的浮沉条件可知，橡皮泥“小碗”漂浮在水面上受到的浮力为
F_{浮} = G = mg = 54×10⁻³ kg×10 N/kg = 0.54 N.
(3)当小碗的上表面恰好与水面相平时，此时的厚度d满足漂浮时的最大厚度，此时排开水的体积为
V_{排} = $\frac{F_{浮}}{\rho_{水}g}$ = $\frac{0.54 N}{1×10^{3} kg/m^{3}×10 N/kg}$ = 5.4×10⁻⁵ m³，
则整个半球的半径为
R = $\sqrt[3]{\frac{3V_{排}}{2\pi}}$ = $\sqrt[3]{\frac{3×5.4×10^{-5} m^{3}}{2×3}}$ = 0.03 m = 3 cm，
空心部分体积为
V_{空} = V_{排} - V = 5.4×10⁻⁵ m³ - 4.5×10⁻⁵ m³ = 0.9×10⁻⁵ m³，
则空心部分半径为
r = $\sqrt[3]{\frac{3V_{空}}{2\pi}}$ = $\sqrt[3]{\frac{3×0.9×10^{-5} m^{3}}{2×3}}$ = $\sqrt[3]{4.5×10^{-6} m^{3}}$ ≈ 1.65×10⁻² m = 1.65 cm，
则厚度d为
d = R - r = 3 cm - 1.65 cm = 1.35 cm，
故橡皮泥“小碗”的厚度d ＜ 1.35 cm，才能够漂浮在水面上.

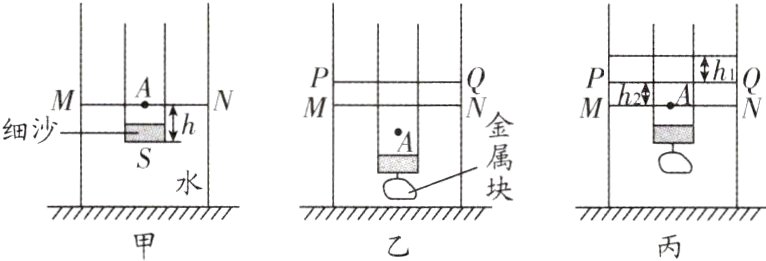
7. 核心素养 科学思维 (2024·安徽中考) 某兴趣小组要测量一金属块的密度，设计了如下方案: 将装有适量细沙的薄壁圆筒，缓慢竖直放入盛有适量水的、水平放置的长方体透明薄壁容器中，待圆筒静止后，在圆筒上对应水面的位置标记一点A，并在长方体容器上标出此时的水位线MN(如图甲所示); 然后将待测金属块用细线悬挂在圆筒下方，缓慢竖直放入水中，圆筒静止后(金属块不接触容器底部)，在长方体容器上标出此时的水位线PQ(如图乙所示); 再向长方体容器中缓慢注水至圆筒上的A点与MN在同一水平面上(如图丙所示). 测出PQ与此时水面的距离为$h_{1}$，与MN的距离为$h_{2}$. 若圆筒的底面积为S，长方体容器的底面积为4S，A点到圆筒底部的竖直距离为h，不计细线的质量和体积，已知$\rho_{水}$和g.
　(1) 求图甲中圆筒和细沙总重力G的大小(用题中给定的物理量符号表示);
　(2) 求金属块的体积V(用题中给定的物理量符号表示):
　(3) 若$h_{1}=0.07 \text{ m}$, $h_{2}=0.03 \text{ m}$, $\rho_{水}=1.0 \times 10^{3} \text{kg/m}^{3}$, 求金属块的密度$\rho$.
　

答案： 7.
(1)ρ_{水}gSh
(2)3Sh₂ - Sh₁
(3)6×10³ kg/m³
解析：
(1)图甲中，圆筒所受浮力等于圆筒和沙子的重力：
G = F_{浮} = ρ_{水}gV_{排} = ρ_{水}gSh.
(2)图乙和图丙相比，浮力相等，V_{排}相等，A点在水面下的深度相等，所以乙图中，A点到水面PQ的距离应该等于h₁ + h₂，A点到MN的距离应该等于h₁，图乙和图甲相比：
ΔV_{排} = ΔV_{筒浸} + V_{金属}.
金属块的体积：
V_{金属} = ΔV_{排} - V_{筒浸} = 4Sh₂ - S(h₁ + h₂) = 3Sh₂ - Sh₁.
(3)由图甲、乙可知，金属块的重力：
G_{金属} = ΔF_{浮} = ρ_{水}g·4Sh₂，
金属块的质量：
m_{金属} = $\frac{G_{金属}}{g}$ = 4ρ_{水}Sh₂.
金属块的密度：
ρ = $\frac{m_{金属}}{V_{金属}}$ = $\frac{4ρ_{水}Sh₂}{3Sh₂ - Sh₁}$ = $\frac{4ρ_{水}h₂}{3h₂ - h₁}$ = $\frac{4×1×10^{3} kg/m^{3}×0.03 m}{3×0.03 m - 0.07 m}$ = 6×10³ kg/m³.